
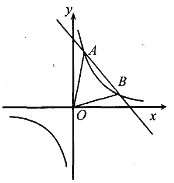
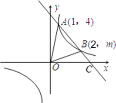
【题目】如图所示,在直角坐标系 xOy 中,一次函数![]() =
=![]() x+b(
x+b(![]() ≠0)的图象与反比例函数
≠0)的图象与反比例函数 ![]()
![]() 的图象交于A(1,4),B(2,m)两点.
的图象交于A(1,4),B(2,m)两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB 的面积;
(3)当 x 的取值范围是 时,![]() x+b>
x+b>![]() (直接将结果填在横线上)
(直接将结果填在横线上)
【答案】(1)![]() ,
,![]() ;(2)3;(3)x<0或
;(2)3;(3)x<0或![]()
【解析】
(1)把(1,4)代入y=![]() ,易求k2,从而可求反比例函数解析式,再把B点坐标代入反比例函数解析式,易求m,然后把A、B两点坐标代入一次函数解析式,易得关于k1、b的二元一次方程,解可求k1、b,从而可求一次函数解析式;
,易求k2,从而可求反比例函数解析式,再把B点坐标代入反比例函数解析式,易求m,然后把A、B两点坐标代入一次函数解析式,易得关于k1、b的二元一次方程,解可求k1、b,从而可求一次函数解析式;
(2)设直线AB与x轴交于点C,再根据一次函数解析式,可求C点坐标,再根据分割法可求△AOB的面积;
(3)观察可知当x<0或1<x<3时,k1x+b>![]() .
.
解:(1)把(1,4)代入y=![]() ,得
,得
k2=4,
∴反比例函数的解析式是y=![]() ,
,
当x=2时,y=![]() ,
,
∴m=2,
把(1,4)、(2,2)代入y1=k1x+b中,得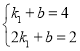 ,
,
解得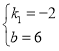 ,
,
∴一次函数的解析式是y=-2x+6;
(2)设直线AB与x轴交于点C,
当y=0时,x=3,
故C点坐标是(3,0),
∴S△AOB=S△AOC-S△BOC=![]() ×3×4-
×3×4-![]() ×3×2=6-3=3;
×3×2=6-3=3;
(3)在第一象限,当1<x<2时,k1x+b>![]() ;
;
还可观察可知,当x<0时,k1x+b>![]() .
.
∴x<0或1<x<2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.当∠MAN绕点A旋转到BM=DN时(如图1),易证BM+DN=MN.
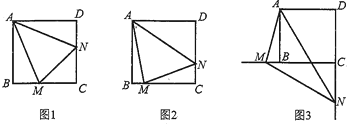
(1)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM、DN和MN之间有怎样的数量关系?写出猜想.并加以证明.
(2)当∠MAN绕点A旋转到如图3位置时,线段BM、DN和MN之间有怎样的数量关系?请写出你的猜想,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
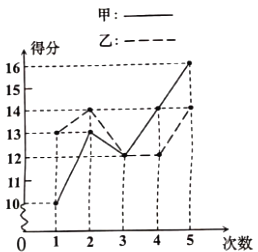
【题目】甲乙两人参加某项体育训练,近期五次测试成绩得分情况如图所示:
(1)分别求出两人得分的平均数;
(2)谁的方差较大?
(3)根据图表和(1)的计算,请你对甲、乙两人的训练成绩作出评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,王老师布置如下任务:
如图1,△ABC中,BC>AB>AC,在BC边上取一点P,使∠APC=2∠ABC.
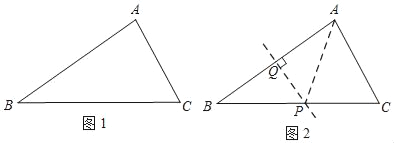
小路的作法如下,如图2:
①作AB边的垂直平分线,交BC于点P;
②连结AP.
所以,∠APC=2∠ABC.
小路的作图依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
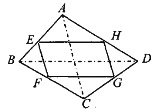
【题目】如图,四边形 ABCD 中,E、F、G、H 分别为各边的中点,顺次连 结 E、F、G、H,把四边形 EFGH 称为中点四边形.连结 AC、BD,容易证明:中点 四边形 EFGH 一定是平行四边形.
(1)如果改变原四边形 ABCD 的形状,那么中点四边形的形状也随之改变,通过探索 可以发现:当四边形 AB CD 的对角线满足 AC=BD 时,四边形 EFGH 为菱形;当四边形ABCD 的对角线满足 时,四边形 EFGH 为矩形;当四边形 ABCD 的对角线满足 时,四边形 EFGH 为正方形.
(2)试证明:S△AEH+S△CFG= ![]() S□ ABCD
S□ ABCD
(3)利用(2)的结论计算:如果四边形 ABCD 的面积为 2012, 那么中点四边形 EFGH 的面积是 (直接将结果填在 横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列说法:①平行四边形既是中心对称图形,又是轴对称图形;②正方形有四条对称轴;③平行四边形相邻两个内角的和等于![]() ;④菱形的面积计算公式,除了“
;④菱形的面积计算公式,除了“![]() 底×高”之外,还有“
底×高”之外,还有“![]() 两对角线之积”;⑤矩形和菱形均是特殊的平行四边形,因此具有平行四边形的所有性质.其中正确的结论的个数有( )
两对角线之积”;⑤矩形和菱形均是特殊的平行四边形,因此具有平行四边形的所有性质.其中正确的结论的个数有( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解七年级学生的身体素质情况,体育老师对该年级部分学生进行了一分钟跳绳次数的测试,并把测试成绩绘制成如图所示的频数表和频数直方图(每组含前一个边界值,不含后一个边界值).


(1)参加测试的学生有多少人?
(2)求![]() ,
,![]() 的值,并把频数直方图补充完整.
的值,并把频数直方图补充完整.
(3)若该年级共有![]() 名学生,估计该年级学生一分钟跳绳次数不少于
名学生,估计该年级学生一分钟跳绳次数不少于![]() 次的人数.
次的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com