
����Ŀ����ͼ��������ABCD�У���MAN=45�㣬��MAN�Ƶ�A˳ʱ����ת���������߷ֱ�CB��DC�������ǵ��ӳ��ߣ��ڵ�M��N.����MAN�Ƶ�A��ת��BM=DNʱ����ͼ1������֤BM+DN=MN.
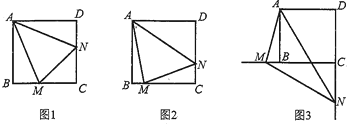
��1������MAN�Ƶ�A��ת��BM��DNʱ����ͼ2),�߶�BM��DN��MN֮����������������ϵ��д������.������֤��.
��2������MAN�Ƶ�A��ת����ͼ3λ��ʱ,�߶�BM��DN��MN֮����������������ϵ����д����IJ��룬������֤��.
���𰸡���1��MN=BM+DN��֤���ԣ���2��MN=DN-BM��֤����.
��������
��1��BM+DN=MN������֤��B��E��M���㹲���ɵõ���AEM�ա�ANM���Ӷ�֤��ME=MN��
��2��DN-BM=MN��֤�������루1�����ƣ�����⣮
�⣺��1��BM+DN=MN������
֤����֤�����£���ͼ2����MB���ӳ����ϣ���ȡBE=DN������AE��
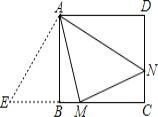
����ABE����ADN��
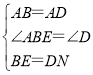 ��
��
���ABE�ա�ADN��SAS����
��AE=AN����EAB=��NAD��
�ߡ�BAD=90������MAN=45����
���BAM+��DAN=45����
���EAB+��BAM=45����
���EAM=��NAM��
����AEM����ANM��
 ��
��
���AEM�ա�ANM��SAS����
��ME=MN��
��ME=BE+BM=DN+BM��
��DN+BM=MN��
��2�����ۣ�DN-BM=MN��
���߶�DN�Ͻ�ȡDQ=BM��
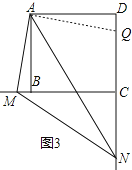
����ADQ����ABM��
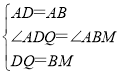 ��
��
���ADQ�ա�ABM��SAS����
���DAQ=��BAM��
���QAN=��MAN��
����AMN����AQN��
 ��
��
���AMN�ա�AQN��SAS����
��MN=QN��
��DN-BM=MN��


 ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˲μ��п��������ԣ��ס��ҡ�����λͬѧ����������ѵ�������һ���˽������������һ���˽��£���ÿλ�����˴����������˵Ļ����Ǿ��ȵģ��ɼ�ʼ�����������Σ�
��1����������״ͼ�оٳ����δ�������п��������
��2�������δ������ص����µĸ��ʣ�
��3�����δ������ص����µĸ��ʴ��Ǵ����ҽ��µĸ��ʴ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,CD��AB,BE��AC,����ֱ�Ϊ��D,��E,BE��CD�ཻ�ڵ�O.��1=��2,��ͼ��ȫ�������ι���( )
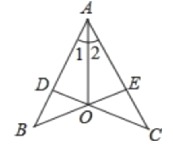
A. 4��B. 3��C. 2��D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�ţ�1����Ϊ���˽�ȫ��ѧ��ϲ���������������ȡȫ�����ķ�����������ƹ��������������ĸ����������ȫ��ѧ������Ȥ���ã����ݵ���Ľ���齨��4����ȤС�飬�����Ƴ���ͼ��ʾ��������������ͳ��ͼ����ͼ�٣��ڣ�Ҫ��ÿλѧ��ֻ��ѡ��һ���Լ�ϲ�������ࣩ���������ͼ���ṩ����Ϣ����������⣺

��1���ţ�1�����ѧ������Ϊ40����������ͳ��ͼ����������
��2������ͳ��ͼ��m=10��n=20����ʾ���������ε�Բ�Ľ���72�ȣ�
��3��������ȤС��4��ѧ������3��1Ů�����ڴ���������ѡ��2��ѧ���μ�ѧУ������ӣ������б�����״ͼ�ķ�����ѡ����2��ѧ��ǡ����1��1Ů�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AC��BDΪ��ֵ��ǽ�棬һ�����Ӵӵ�O���𣬵�����ǽ��AC��ʱ�����ӵ���һ�����ڵ�A������ʱ��AOC=60�㣬������ǽ��BD��ʱ�����ӵ���һ�����ڵ�B������ʱ��BOD=45�㣬��OD=3![]() �ף�
�ף�
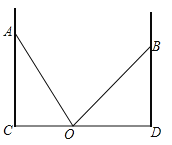
��1�������ӵij�����2����OC��AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��С���ڴ�¥30�ߣ���PH��30�ף��Ĵ���P�����й۲⣬���ɽ����A���ĸ���Ϊ15�㣬ɽ��B���ĸ���Ϊ60�㣬��֪��ɽ�µ��¶�i����tan��ABC��Ϊ1��![]() ����P��H��B��C��A��ͬһ��ƽ���ϣ���H��B��C��ͬһ��ֱ���ϣ���PH��HC��
����P��H��B��C��A��ͬһ��ƽ���ϣ���H��B��C��ͬһ��ֱ���ϣ���PH��HC��

��1��ɽ���½ǣ�����ABC���Ķ������� �ȣ�
��2����ɽ��A��B�����ľ��루�����ȷ��0.1�ף���
���ο����ݣ�![]() ��1.414��
��1.414��![]() ��1.732��
��1.732��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AD=![]() AB����BAD��ƽ���߽�BC�ڵ�E��DH��AE�ڵ�H������BH���ӳ���CD�ڵ�F������DE��BF�ڵ�O�����н��ۣ��١�AED=��CED����OE=OD����BH=HF����BC��CF=2HE����AB=HF��������ȷ���У� ��
AB����BAD��ƽ���߽�BC�ڵ�E��DH��AE�ڵ�H������BH���ӳ���CD�ڵ�F������DE��BF�ڵ�O�����н��ۣ��١�AED=��CED����OE=OD����BH=HF����BC��CF=2HE����AB=HF��������ȷ���У� ��

A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD�У���BAD��60�㣬��E��F�ֱ���AB��AD���������㣬��AE��DF������BF��DE�ཻ�ڵ�G������CG����BD�ཻ��H��
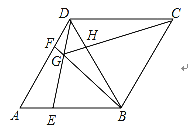
��1�����BGE�Ĵ�С����2����֤��GCƽ�֡�BGD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
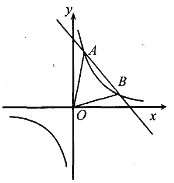
����Ŀ����ͼ��ʾ����ֱ������ϵ xOy �У�һ�κ���![]() ��
��![]() x��b��
x��b��![]() ��0����ͼ���뷴��������
��0����ͼ���뷴�������� ![]()
![]() ��ͼ����A(1��4)��B(2��m)���㣮
��ͼ����A(1��4)��B(2��m)���㣮
(1)��ȷ������������������һ�κ����ı���ʽ��
(2)����AOB �������
(3)�� x ��ȡֵ��Χ�� ʱ��![]() x��b>
x��b>![]() ��ֱ�ӽ�������ں����ϣ�
��ֱ�ӽ�������ں����ϣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com