
【题目】在ABCD中,∠ADC的平分线交直线BC于点E,交直线AB于点F.
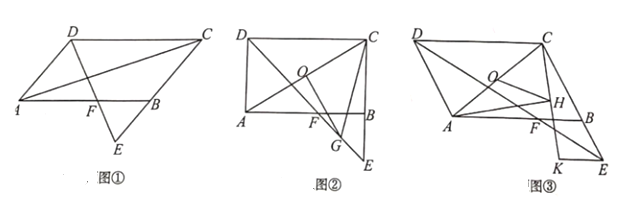
(1)如图①,证明:BE=BF.
(2)如图②,若∠ADC=90°,O为AC的中点,G为EF的中点,试探究OG与AC的位置关系,并说明理由.
(3)如图③,若∠ADC=60°,过点E作DC的平行线,并在其上取一点K(与点F位于直线BC的同侧),使EK=BF,连接CK,H为CK的中点,试探究线段OH与HA之间的数量关系,并对结论给予证明.
【答案】(1)详见解析;(2)GO⊥AC;(3)AH=![]() OH
OH
【解析】
(1)根据平行线的性质得出∠E=∠ADF,∠EFB=∠EDC,再利用ED平分∠ADC,即可解答
(2)连接BG,AG,根据题意得出四边形ABCD是矩形,再利用矩形的性质,证明△ABG≌△CEG,即可解答
(3)连接AK,BK,FK,先得出四边形BFKE是菱形,,再利用菱形的性质证明△KBE,△KBF都是等边三角形,再利用等边三角形的性质得出△ABK≌△CEK,最后利用三角函数即可解答
(1)证明:如图①中,因为四边形ABCD为平行四边形,
所以,AD∥EC,AB∥CD,
所以,∠E=∠ADF,∠EFB=∠EDC,
因为ED平分∠ADC,
所以,∠ADF=∠EDC,
所以,∠E=∠EFB,
所以,BE=BF
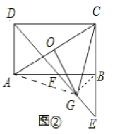
(2)解:如图⊙中,结论:GO⊥AC
连接BG,AG
∵四边形ABCD是平行四边形,∠ADC=90°,
四边形ABCD是矩形,
∠ABC=∠ABE=90°,
由(1)可知:BE=BF,
∵∠EBF=90°,EG=FG,
∴∠E=45°,∠GBF=∠GBE=45°,BG=GE=GF,
∵∠DCE=90°
∴∠E=∠EDC=45°,
∴DC=CE=BA,
∵∠ABG=∠E=45°,AB=EC,BG=EG,
∴△ABG≌△CEG(SAS),
∵GA=GC
∴AO=OC.
∴GO⊥AC
(3)解:如图⊙中,连接AK,BK,FK

∵BF=EK,BF∥EK,
∴四边形BFKE是平行四边形,
∵BF=BE,
∴四边形BFKE是菱形,
∵边形ABCD是平行四边形,
∴∠ADC=∠ABC=60°,∠DCB=∠DAB=120°
∴∠EBF=120°,
∴∠KBE=∠KBF=60°
BF=BE=FK=EK,
∴△KBE,△KBF都是等边三角形,
∴∠ABK=∠CEK=60°,∠FEB=∠FEK=30
∴∠CDE=∠CED=30°
∴CD=CE=BA,
∵BK=EK,
∴△ABK≌△CEK(SAS)
∴AK=CK,∠AKB=∠CKB
∴∠AKC=∠BKE=60°
∴△ACK是等边三角形
∵OA=OC,CH=HK
∴AK=2OH,AH⊥CK,
∴AH=AK·cos30°=![]() AK
AK
∴AH=![]() OH.
OH.


科目:初中数学 来源: 题型:
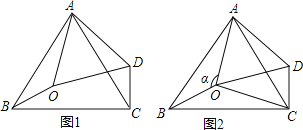
【题目】如图1,在△ABC中,∠BAC=60°,点0是△ABC内一点,△AB0![]() △ACD,连接OD.
△ACD,连接OD.
(1)求证△AOD为等边三角形。
(2)如图2,连接OC,若∠BOC=130°,∠AOB=![]() .
.
①求∠OCD的度数
②当△OCD是等腰三角形时,求∠![]() 的度数
的度数
 、
、
查看答案和解析>>
科目:初中数学 来源: 题型:
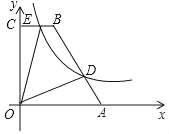
【题目】如图,在四边形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且![]() ,双曲线y=
,双曲线y=![]() (k>0)经过点D,交BC于点E
(k>0)经过点D,交BC于点E
(1)求双曲线的解析式;
(2)求四边形ODBE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2014贵州黔东南)黔东南州某超市计划购进一批甲、乙两种玩具,已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元,2件甲种玩具的进价与3件乙种玩具的进价的和为141元.
(1)求每件甲种、乙种玩具的进价分别是多少元;
(2)如果购进甲种玩具有优惠,优惠方法是:购进甲种玩具超过20件,超出部分可以享受7折优惠.若购进x(x>0)件甲种玩具需要花费y元,请你求出y与x的函数关系式;
(3)在(2)的条件下,超市决定在甲、乙两种玩具中选购其中一种,且数量超过20件,请你帮助超市判断购进哪种玩具省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知C为线段AB的中点,E为线段AB上的点,点D为线段AE的中点.
![]()
(1)若线段AB=a,CE=b,|a﹣17|+(b﹣5.5)2=0,求线段AB、CE的长;
(2)如图1,在(1)的条件下,求线段DE的长;
(3)如图2,若AB=20,AD=2BE,求线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
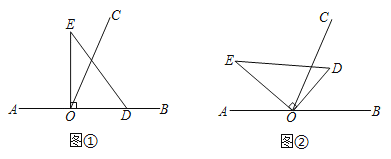
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,把图①中直角三角板DOE绕点O逆时针方向以10°每秒的速度转动,求至少转多少秒能使OC恰好平分∠BOE?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,将边长为 9cm 的正方形纸片 ABCD 折叠,使得点 A 落在边 CD 上的 E 点,折痕为 MN.若 CE 的长为 6cm,则 MN 的长为_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”倡议提出3年多来,交通、通信、能源等各项相关建设取得积极进展,也为增进各国民众福祉提供了新的发展机遇.如图,是“一带一路”沿线部分国家的通信设施现状统计图.观察图,请回答下列问题:
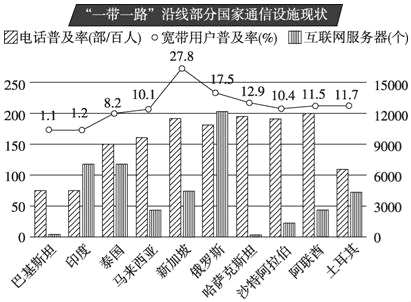
(1)在这10个国家中,互联网服务器拥有个数最多的国家是 ;
(2)在这10个国家中,每100人拥有电话数量最接近150部的国家是 ;
(3)在这10个国家中,宽带用户普及率最高的国家是 ,普及率为 ;
(4)在这10个国家中,宽带用户普及率的中位数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC,∠C=90°.
(1)求作:△ABC的内切圆⊙O;(尺规作图,不写作法,保留痕迹)
(2)在(1)中,∠AOB的度数为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com