
【题目】如图,已知Rt△ABC,∠C=90°.
(1)求作:△ABC的内切圆⊙O;(尺规作图,不写作法,保留痕迹)
(2)在(1)中,∠AOB的度数为 .

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在ABCD中,∠ADC的平分线交直线BC于点E,交直线AB于点F.
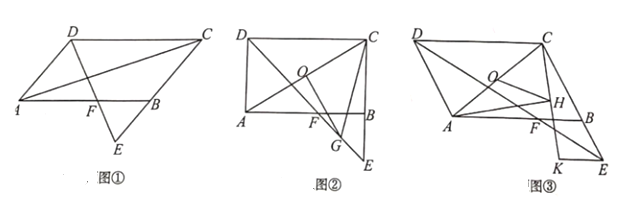
(1)如图①,证明:BE=BF.
(2)如图②,若∠ADC=90°,O为AC的中点,G为EF的中点,试探究OG与AC的位置关系,并说明理由.
(3)如图③,若∠ADC=60°,过点E作DC的平行线,并在其上取一点K(与点F位于直线BC的同侧),使EK=BF,连接CK,H为CK的中点,试探究线段OH与HA之间的数量关系,并对结论给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE,CF交于点D,则下列结论中不正确的是( )

A. △ABE≌△ACF B. 点D在∠BAC的平分线上
C. △BDF≌△CDE D. D是BE的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[ 问题提出 ]
一个边长为 ncm(n3)的正方体木块,在它的表面涂上颜色,然后切成边长为1cm的小正方体木块,没有涂上颜色的有多少块?只有一面涂上颜色的有多少块?有两面涂上颜色的有多少块?有三面涂上颜色的多少块?
[ 问题探究 ]
我们先从特殊的情况入手
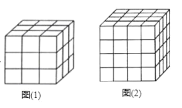
(1)当n=3时,如图(1)
没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有1×1×1=1个小正方体;
一面涂色的:在面上,每个面上有1个,共有6个;
两面涂色的:在棱上,每个棱上有1个,共有12个;
三面涂色的:在顶点处,每个顶点处有1个,共有8个.
(2)当n=4时,如图(2)
没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有2×2×2=8个小正方体:
一面涂色的:在面上,每个面上有4个,正方体共有 个面,因此一面涂色的共有 个;
两面涂色的:在棱上,每个棱上有2个,正方体共有 条棱,因此两面涂色的共有 个;
三面涂色的:在顶点处,每个顶点处有1个,正方体共有 个顶点,因此三面涂色的共有 个…
[ 问题解决 ]
一个边长为ncm(n3)的正方体木块,没有涂色的:把这个正方形的表层“剥去”剩下的正方体,有______个小正方体;一面涂色的:在面上,共有______个; 两面涂色的:在棱上,共有______个; 三面涂色的:在顶点处,共______个。
[ 问题应用 ]
一个大的正方体,在它的表面涂上颜色,然后把它切成棱长1cm的小正方体,发现有两面涂色的小正方体有96个,请你求出这个大正方体的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=﹣x+2与x轴、y轴分别交于点A、点C,抛物线经过点A、点C,且与x轴的另一个交点为B(﹣1,0).
(1)求抛物线的解析式;
(2)点D为第一象限内抛物线上的一动点.
①如图1,若CD=AD,求点D的坐标;
②如图2,BD与AC交于点E,求S△CDE:S△CBE的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三位自然数m,将它任意两个数位上的数字对调后得一个首位不为0 的新三位自然数 m’( m’可以与m相同),记m’=![]() ,在 m’ 所有的可能情况中,当|a+2b-c| 最小时,我们称此时的m’ 是m 的“幸福美满数”,并规定K (m) = a2 +2b2 -c2.例如:318按上述方法可得新数有:381、813 、138 ;因为|3+2
,在 m’ 所有的可能情况中,当|a+2b-c| 最小时,我们称此时的m’ 是m 的“幸福美满数”,并规定K (m) = a2 +2b2 -c2.例如:318按上述方法可得新数有:381、813 、138 ;因为|3+2![]() 8-1|= 18 ,|8+ 2
8-1|= 18 ,|8+ 2![]() 1-3|=7,|1 +2
1-3|=7,|1 +2![]() 3-8|=1,1< 7<18 ,所以138 是318的“幸福美满数”,K(318)=|12+2
3-8|=1,1< 7<18 ,所以138 是318的“幸福美满数”,K(318)=|12+2![]() 32-82|=-45.
32-82|=-45.
(1)若三位自然数t的百位上的数字与十位上的数字都为n(1≤n ≤ 9 ,n为自然数),个位上的数字为0 ,求证:K (t )= 0;
(2)设三位自然数s=100+10x + y(1≤ x ≤ 9,1≤y≤9, ,x y 为自然数) ,且x<y .交换其个位与十位上的数字得到新数s’,若19s+8s’=3888,那么我们称s为“梦
想成真数”,求所有“梦想成真数”中K (s )的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,已知∠BAD=120°,∠EGF=60°, ∠EGF的顶点G在菱形对角线AC上运动,角的两边分别交边BC、CD于E、F.
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/STEM/6b570bc424f747a8be031e9f971720ec.png]
(1)如图甲,当顶点G运动到与点A重合时,求证:EC+CF=BC;
(2)知识探究:
①如图乙,当顶点G运动到AC的中点时,请直接写出线段EC、CF与BC的数量关系(不需要写出证明过程);
②如图丙,在顶点G运动的过程中,若![]() ,探究线段EC、CF与BC的数量关系;
,探究线段EC、CF与BC的数量关系;
(3)问题解决:如图丙,已知菱形的边长为8,BG=7,CF=![]() ,当
,当![]() >2时,求EC的长度。
>2时,求EC的长度。
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/STEM/1671b8ec524a49feac7097357d4ff9a8.png]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com