
【题目】如图,菱形ABCD中,已知∠BAD=120°,∠EGF=60°, ∠EGF的顶点G在菱形对角线AC上运动,角的两边分别交边BC、CD于E、F.
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/STEM/6b570bc424f747a8be031e9f971720ec.png]
(1)如图甲,当顶点G运动到与点A重合时,求证:EC+CF=BC;
(2)知识探究:
①如图乙,当顶点G运动到AC的中点时,请直接写出线段EC、CF与BC的数量关系(不需要写出证明过程);
②如图丙,在顶点G运动的过程中,若![]() ,探究线段EC、CF与BC的数量关系;
,探究线段EC、CF与BC的数量关系;
(3)问题解决:如图丙,已知菱形的边长为8,BG=7,CF=![]() ,当
,当![]() >2时,求EC的长度。
>2时,求EC的长度。
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/STEM/1671b8ec524a49feac7097357d4ff9a8.png]
【答案】(1)证明见解析(2)①线段EC,CF与BC的数量关系为:CE+CF=![]() BC.②CE+CF=
BC.②CE+CF=![]() BC(3)
BC(3)![]()
【解析】分析:(1)利用包含60°角的菱形,证明△BAE≌△CAF,可求证.(2)由特殊到一般,证明△CAE′∽△CAE,从而可以得到EC、CF与BC的数量关系.(3) 连接BD与AC交于点H,利用三角函数BH ,AH,CH的长度,最后求BC长度.
详解:
(1)证明:∵四边形ABCD是菱形,∠BAD=120°,
∴∠BAC=60°,∠B=∠ACF=60°,AB=BC,AB=AC,
∵∠BAE+∠EAC=∠EAC+∠CAF=60°,
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/EXPLANATION/d76d152670f6452b8f83f62ba9f41a35.png]
∴∠BAE=∠CAF,
在△BAE和△CAF中,
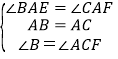 ,
,
∴△BAE≌△CAF,
∴BE=CF,
∴EC+CF=EC+BE=BC,
即EC+CF=BC;
(2)知识探究:
①线段EC,CF与BC的数量关系为:CE+CF=![]() BC.
BC.
②CE+CF=![]() BC.
BC.
理由如下:
过点A作AE′∥EG,AF′∥GF,分别交BC、CD于E′、F′.
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/EXPLANATION/f233fd78cd694e2aa6ff6f6aea848566.png]
类比(1)可得:E′C+CF′=BC,
∵AE′∥EG,∴△CAE′∽△CAE,
∴![]() ,∴CE=
,∴CE=![]() CE′,
CE′,
同理可得:CF=![]() CF′,
CF′,
∴CE+CF=![]() CE′+
CE′+![]() CF′=
CF′=![]() (CE′+CF′)=
(CE′+CF′)=![]() BC,
BC,
即CE+CF=![]() BC;
BC;
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/EXPLANATION/db33a252ee584146a248213b3c17919b.png]
(3)连接BD与AC交于点H,如图所示:
在Rt△ABH中,∵AB=8,∠BAC=60°,
∴BH=ABsin60°=8×![]() =
=![]() ,
,
AH=CH=ABcos60°=8×![]() =4,
=4,
∴GH=![]() =
=![]() =1,
=1,
∴CG=4-1=3,
∴![]() ,
,
∴t=![]() (t>2),
(t>2),
由(2)②得:CE+CF=![]() BC,
BC,
∴CE=![]() BC -CF=
BC -CF=![]() ×8-
×8-![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:
∵![]() ,
,![]() ,
,![]() ,……
,……![]() ,
,
∴![]()
=![]()
=![]() =
=![]() .
.
解答下列问题:
(1)在和式![]() 中,第6项为______,第n项是__________.
中,第6项为______,第n项是__________.
(2)上述求和的想法是通过逆用分式减法法则,将和式中的各分数转化为两个数之差,使得除首末两项外的中间各项的和为_______,从而达到求和的目的.
(3)受此启发,请你解下面的方程:
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
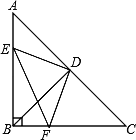
【题目】已知:如图,在△ABC中,∠ABC=90°,AB=BC,D是AC的中点,点E在AC上,点F在BC上,且AE=BF.
(1)求证:DE=DF;
(2)连接EF,求∠DEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.
(1)自己画出图形并解答:A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭受这次台风影响有多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
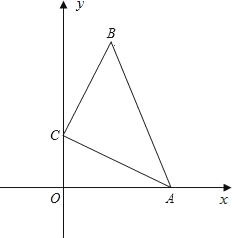
【题目】如图,在直角坐标系中,△ABC满足∠BCA=90°,AC=BC=![]() ,点A、C分别在x轴和y轴上,当点A从原点开始沿x轴的正方向运动时,则点C始终在y轴上运动,点B始终在第一象限运动.
,点A、C分别在x轴和y轴上,当点A从原点开始沿x轴的正方向运动时,则点C始终在y轴上运动,点B始终在第一象限运动.
(1)当AB∥y轴时,求B点坐标.
(2)随着A、C的运动,当点B落在直线y=3x上时,求此时A点的坐标.
(3)在(2)的条件下,在y轴上是否存在点D,使以O、A、B、D为顶点的四边形面积是4?如果存在,请直接写出点D的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com