
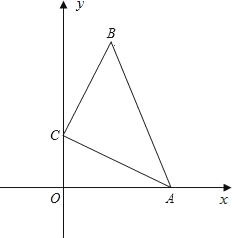
����Ŀ����ͼ����ֱ������ϵ�У���ABC�����BCA��90�㣬AC��BC��![]() ����A��C�ֱ���x���y���ϣ�����A��ԭ�㿪ʼ��x����������˶�ʱ�����Cʼ����y�����˶�����Bʼ���ڵ�һ�����˶���
����A��C�ֱ���x���y���ϣ�����A��ԭ�㿪ʼ��x����������˶�ʱ�����Cʼ����y�����˶�����Bʼ���ڵ�һ�����˶���
��1����AB��y��ʱ����B�����꣮
��2������A��C���˶�������B����ֱ��y��3x��ʱ�����ʱA������꣮
��3���ڣ�2���������£���y�����Ƿ���ڵ�D��ʹ��O��A��B��DΪ������ı��������4��������ڣ���ֱ��д����D�����ꣻ��������ڣ���˵�����ɣ�
���𰸡���1����B����Ϊ��![]() ��
��![]() ����2����A��2��0������3�����ڵ�D����D����Ϊ��0����1����0��2��.
����2����A��2��0������3�����ڵ�D����D����Ϊ��0����1����0��2��.
��������
��1�����ݹ��ɶ������ɵ�AB�ij������ݹ��ɶ������ɵ�AO�ij����ɵ�B�����ꣻ
��2������ȫ�������ε��ж������ʣ��ɵ�BE��OC��x��EC��OA��x�����ݹ��ɶ������ɵ�x�ij����ɵ�A�����ꣻ
��3���������ۣ���D��y����������ϣ���D��y��ĸ������ϣ���������ĺͲ�ɵù���y�ķ��̣����ݽⷽ�̣��ɵô𰸣�
��1���ߡ�BCA��90�㣬AC��BC��![]() ��
��
���BAC��45�㣬AB��![]() ��
��![]()
��AB��y�ᣬ
���BAO��90�㣽��COA
���CAO��45�㣽��OCA
��CO��AO
��AO2+CO2��AC2��
��2AO2��5
��AO��![]()
���B������![]() ��
��![]() ��
��
��2����ͼ������B����BE��y�ᣬ����Ϊ��E��
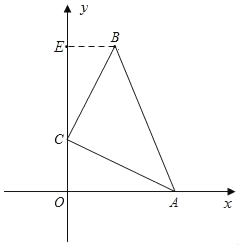
�ߡ�BCE+��ACO��90�㣬��ACO+��CAO��90��
���BCE����CAO����AC��BC����BEO����AOC
���AOC�ա�CEB��AAS��
��BE��CO��AO��CE
�ߵ�B����ֱ��y��3x��
����B��x��3x��
��BE��x��OC��OE��3x��
��CE��OA��2x��
��OA2+OC2��AC2
�ࣨ2x��2+x2��5
��x��1
��OA��2x��2
���A��2��0��
��3�����D��0��y��
����D��y���������ϣ���ͼ������OB��
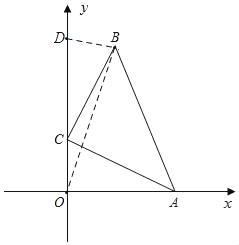
��S�ı���ABDO��S��AOB+S��BDO��4
��![]() ��y��1+
��y��1+![]() ��2��3��4
��2��3��4
��y��2
���D��0��2��
����D��y�Ḻ�����ϣ���ͼ������OB��

��S�ı���ABDO��S��AOB+S��ADO��4
��![]() ��2��3+
��2��3+![]() ��2������y����4
��2������y����4
��y����1
���D������0����1��.
����ڵ�D����D����Ϊ��0��2����0����1��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���֪��BAD=120�㣬��EGF=60��, ��EGF�Ķ���G�����ζԽ���AC���˶����ǵ����߷ֱ�BC��CD��E��F��
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/STEM/6b570bc424f747a8be031e9f971720ec.png]
��1����ͼ�ף�������G�˶������A�غ�ʱ����֤��EC+CF=BC��
��2��֪ʶ̽����
����ͼ�ң�������G�˶���AC���е�ʱ����ֱ��д���߶�EC��CF��BC��������ϵ������Ҫд��֤�����̣���
����ͼ�����ڶ���G�˶��Ĺ����У���![]() ��̽���߶�EC��CF��BC��������ϵ��
��̽���߶�EC��CF��BC��������ϵ��
��3������������ͼ������֪���εı߳�Ϊ8��BG=7��CF=![]() ����
����![]() ��2ʱ����EC�ij��ȡ�
��2ʱ����EC�ij��ȡ�
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/STEM/1671b8ec524a49feac7097357d4ff9a8.png]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ͼ���ṩ����Ϣ,�ش���������

��1��һ��ůƿ��һ��ˮ���ֱ��Ƕ���Ԫ?
��2���ס��������̳�ͬʱ����ͬ����ůƿ��ˮ��,Ϊ��ӭ������,�����̳����ڸ�����,���̳��涨�� ��������Ʒ������������̳��涨����һ��ůƿ����һ��ˮ������ij��λ��Ҫ��4��ůƿ��15��ˮ��������ѡ���ļ��̳���������㣬��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���������ϱ���:�������������ʱ��t(h)����������Ĺ�ʽ������:t2=![]() ,����d(km)�����������ֱ��.
,����d(km)�����������ֱ��.
(1)������������ֱ��Ϊ9km,��ô�ⳡ�����Լ�ܳ����ʱ��?
(2)���һ�����������1h,��ô�ⳡ���������ֱ����Լ�Ƕ���(�����ȷ��0.1km)?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳���2���ף�E��CD�ߵ��е㣬F��BC�����ƶ�����AEǡ��ƽ�֡�FADʱ��CF��_____���ף�
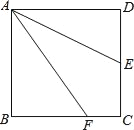
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C��90�㣬ADƽ�֡�BAC��DE��AB��E�������н��ۣ���DE��CD����ADƽ�֡�CDE���ۡ�BAC����BDE����BE+AC��AB��������ȷ���ǣ� ��

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�D��BC���е㣬��D���ֱ��GF��AC��F����AC��ƽ����BG��G�㣬DE��DF����AB�ڵ�E������EG��EF��

��1����֤��BG��CF��
��2�������ж�BE+CF��EF�Ĵ�С��ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڽⲻ��ʽ|x+1|��2ʱ�����ǿ��Բ�������Ľ����
����x+1��0ʱ��|x+1|��x+1��
����ԭ����ʽ��x+1��2����ɵò���ʽ��![]()
���ò���ʽ��Ľ⼯Ϊx��1��
����x+1��0ʱ��|x+1|����(x+1)��
����ԭ����ʽ�é�(x+1)��2����ɵò���ʽ��![]()
���ò���ʽ��Ľ⼯Ϊx����3��
����������ԭ����ʽ�Ľ⼯Ϊx��1��x����3��
��������������������Խⲻ��ʽ|x��2|��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������ֻ��շ�����![]() ���ַ�ʽ����������ѣ����û�����ѡ��һ��
���ַ�ʽ����������ѣ����û�����ѡ��һ��
A�������0Ԫ������绰�Ʒ�0.15Ԫ/��
B�������15Ԫ������绰�Ʒ�0.1Ԫ/��
��1��ij�û�ij�´��ֻ�100���ӣ���������ַ�ʽ���ɷѶ���Ԫ��
��2��ij�û�ij�´��ֻ�x���ӣ�����д�����ַ�ʽ�¸��û�Ӧ�ɸ��ķ��ã�
��3����ij�û�����һ�����ڴ��ֻ�15Сʱ������Ϊ���ַ�ʽ�����㣿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com