
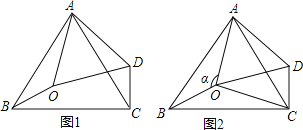
【题目】如图1,在△ABC中,∠BAC=60°,点0是△ABC内一点,△AB0![]() △ACD,连接OD.
△ACD,连接OD.
(1)求证△AOD为等边三角形。
(2)如图2,连接OC,若∠BOC=130°,∠AOB=![]() .
.
①求∠OCD的度数
②当△OCD是等腰三角形时,求∠![]() 的度数
的度数
 、
、
【答案】(1)见解析;.(2)①∠OCD=70°;②可以是130°,100°,115°.
【解析】
(1)根据全等三角形得到AO=AD,∠BAO=∠CAD,由∠BAC=60°,求得∠OAD=60°,即可得到结论;
(2)①根据△AOD为等边三角形,求得∠AOD=∠ADO=60°,求得∠DOC=360°-α-130°-60°=170°-α,根据全等三角形的性质得到∠ADC=∠AOB=α,于是得到∠OCD=180°-∠DOC-∠ODC=70°;②当△OCD是等腰三角形时,(Ⅰ)当OD=OC,由∠DOC=170°-α,得到∠OCD=∠ODC= ![]() α+5°,列方程得到α=130°(Ⅱ)当OD=CD,于是得到∠OCD=∠COD=170°-α;求得∠ODC=180°-2×170°+2α=2α-160°,列方程即可得到α=100°;(Ⅲ)当OC=CD,于是得到∠ODC=∠COD=170°-α,列方程即可得到α=115°.
α+5°,列方程得到α=130°(Ⅱ)当OD=CD,于是得到∠OCD=∠COD=170°-α;求得∠ODC=180°-2×170°+2α=2α-160°,列方程即可得到α=100°;(Ⅲ)当OC=CD,于是得到∠ODC=∠COD=170°-α,列方程即可得到α=115°.
(1)证明:∵△ABO≌△ACD
∴∠OAB=∠CAD
∴AO=AD
∴∠OAB+∠OAC=∠OAC+∠CAD=60°
△AOD为等边三角形.
(2)①∵△AOD为等边三角形,
∴∠AOD=∠ADO=60°,
∵∠BOC=130°,∠AOB=∠α,
∴∠DOC=360°α130°60°=170°α,
∵△ABO≌△ACD,
∴∠ADC=∠AOB=α,
∴∠ODC=α60°,
∴∠OCD=180°∠DOC∠ODC=70°;
②当△OCD是等腰三角形时,
(Ⅰ)当OD=OC,∵∠DOC=170°α,
∴∠OCD=∠ODC=![]() α+5°,
α+5°,
∴60°+![]() α+5°=α,
α+5°=α,
解得:α=130°
(Ⅱ)当OD=CD,∴∠OCD=∠COD=170°α;
∴∠ODC=180°2×170°+2α=2α160°,
∴60°+2α160°=α,
解得:α=100°;
(Ⅲ)当OC=CD,∴∠ODC=∠COD=170°α,
∴170°α+60°=α,
解得:α=115°.
综上所述:当△OCD是等腰三角形时,∠α的度数为:130°,100°,115°.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 同时从点
同时从点![]() 出发,以相同的速度分别沿折线
出发,以相同的速度分别沿折线![]() 、射线
、射线![]() 运动,连接
运动,连接![]() .当点
.当点![]() 到达点
到达点![]() 时,点
时,点![]() 、
、![]() 同时停止运动.设
同时停止运动.设![]() ,
,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
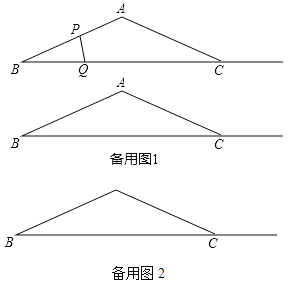
(1)求![]() 长;
长;
(2)求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(3)请直接写出![]() 为等腰三角形时
为等腰三角形时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB的边OA上有一动点P,从距离O点18cm的点M处出发,沿线段MO,射线OB运动,速度为2cm/s;动点Q从点O出发,沿射线OB运动,速度为1cm/s.P、Q同时出发,设运动时间是t(s).
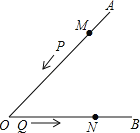
(1)当点P在MO上运动时,PO= cm (用含t的代数式表示);
(2)当点P在MO上运动时,t为何值,能使OP=OQ?
(3)若点Q运动到距离O点16cm的点N处停止,在点Q停止运动前,点P能否追上点Q?如果能,求出t的值;如果不能,请说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,最省事的办法是( )
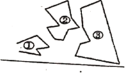
A. 带①去B. 带②去C. 带③去D. 带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进A、B两种商品共100件,花费3100元,其进价和售价如下表;
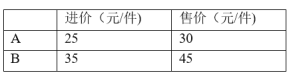
(1)A、B两种商品分别购进多少件?
(2)两种商品售完后共获取利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段AB=20cm.
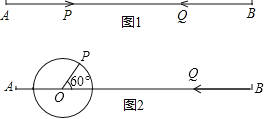
(1)如图1,点P沿线段AB自A点向B点以2厘米/秒运动,点Q沿线段BA自B点向A点以3厘米/秒运动,经过________秒,点P、Q两点能相遇.
(2)如图1,点P沿线段AB自A点向B点以2厘米/秒运动,同时点Q沿线段BA自B点向A点以3厘米/秒运动,问再经过几秒后P、Q相距5cm?
(3)如图2,AO=4cm,PO=2cm,∠POB=60°,点P绕着点O以60°/秒的速度逆时针旋转一周停止,同时点Q沿直线BA自B点向A点运动,假若点P、Q两点能相遇,求点Q运动的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连结BO,若S△AOB=4.

(1)求该反比例函数的解析式和直线AB的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·漳州)(满分8分)漳州市某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:

(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有_ ▲ 人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠ADC的平分线交直线BC于点E,交直线AB于点F.
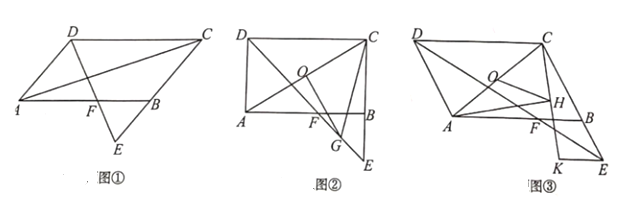
(1)如图①,证明:BE=BF.
(2)如图②,若∠ADC=90°,O为AC的中点,G为EF的中点,试探究OG与AC的位置关系,并说明理由.
(3)如图③,若∠ADC=60°,过点E作DC的平行线,并在其上取一点K(与点F位于直线BC的同侧),使EK=BF,连接CK,H为CK的中点,试探究线段OH与HA之间的数量关系,并对结论给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com