
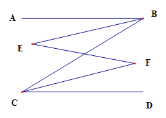
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 同时从点
同时从点![]() 出发,以相同的速度分别沿折线
出发,以相同的速度分别沿折线![]() 、射线
、射线![]() 运动,连接
运动,连接![]() .当点
.当点![]() 到达点
到达点![]() 时,点
时,点![]() 、
、![]() 同时停止运动.设
同时停止运动.设![]() ,
,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
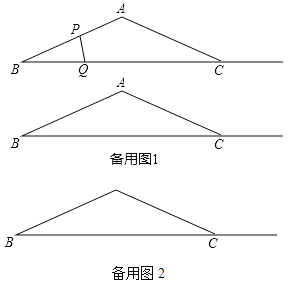
(1)求![]() 长;
长;
(2)求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(3)请直接写出![]() 为等腰三角形时
为等腰三角形时![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2) ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)过点A作AM⊥BC于点M,由等腰三角形的性质可得∠B=∠C=30°,BM=CM=![]() BC,由直角三角形的性质可得BM=2
BC,由直角三角形的性质可得BM=2![]() ,即可求BC的值;
,即可求BC的值;
(2)分点P在AB上,点P在AC上,点Q在BC的延长线上时,三种情况讨论,由三角形的面积公式可求S关于x的函数关系式;
(3)分两种情况讨论,由等腰三角形的性质可求解.
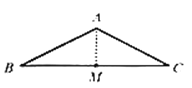
解:(1)过点![]() 作
作![]() 于点
于点![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
(2)因为点![]() ,
,![]() 同时出发且速度相同,所以两点运动的路程相同
同时出发且速度相同,所以两点运动的路程相同
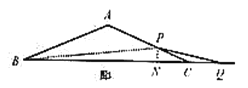
情况①:当![]() 时,此时点
时,此时点![]() 在线段
在线段![]() 上,如图1
上,如图1
过点![]() 作
作![]() 于点
于点![]() ,
,
在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() 与
与![]() 重叠部分的面积
重叠部分的面积![]() .
.
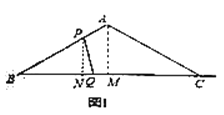
情况②:当![]() 时,此时点
时,此时点![]() 在线段
在线段![]() 上,如图2
上,如图2
过点![]() 作
作![]() 于点
于点![]() ,
,
此时,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() 与
与![]() 重叠部分的面积
重叠部分的面积![]() .
.
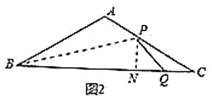
情况③:当![]() 时,此时点
时,此时点![]() 在线段
在线段![]() 上,
上,![]() 在线段
在线段![]() 延长线上,如图3
延长线上,如图3
过点![]() 作
作![]() 于点
于点![]() ,
,
由情况②同理可得:![]() ,
,
∴![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() 的面积,
的面积,
则![]()
![]() .
.
综上所述:![]() 与
与![]() 重叠部分的面积
重叠部分的面积 .
.
(3)![]() 或
或![]()
①当点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上时,
上时,![]() 不可能是等腰三角形.
不可能是等腰三角形.
②当点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上时,
上时,![]() ,
,![]() ,
,
③当点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线时,
的延长线时,![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】完成下面的推理过程.
如图,AB∥CD,BE、CF分别是∠ABC和∠BCD的平分线.求证:∠E=∠F
证明:∵AB∥CD(已知)
∴∠ABC=∠BCD( )
∵BE、CF分别是∠ABC和∠BCD的平分线(已知)
∴∠CBE=![]() ∠ABC,∠BCF=
∠ABC,∠BCF=![]() ∠BCD( )
∠BCD( )
∴∠CBE=∠BCF( )
∴BE∥CF( )
∴∠E=∠F( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,有一个长方形被分割成了6个大小不同的正方形,其中最小正方形的边长是3,则该长方形长是___________;将同一个长方形作如图2分割,分割成左上角的长方形G、右下角的长方形H以及7张长宽相同的小长方形M(小长方形M如图3所示),当长方形G与长方形H的周长相等时,小长方形M的宽是________________.
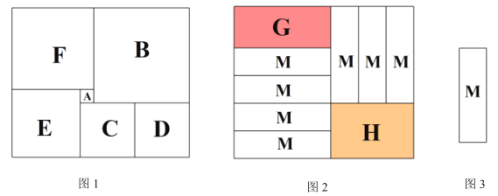
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表 示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中错误的是( )
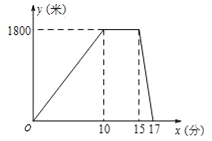
A.小明在公园休息了5分钟
B.小明乘出租车用了17分
C.小明跑步的速度为180米/分
D.出租车的平均速度是900米/分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为鼓励市民节约用水,自来水公司按分段收费标准收费,如图反映的是每月水费![]() (元)与用水量
(元)与用水量![]() (吨)之间的函数关系.
(吨)之间的函数关系.
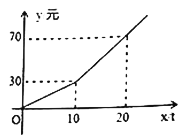
(1)当用水量超过10吨时,求![]() 关于
关于![]() 的函数解析式(不必写自变量取值范围);
的函数解析式(不必写自变量取值范围);
(2)按上述分段收费标准小聪家三、四月份分别交水费38元和27元,问四月份比三月份节约用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.
(1)当点C,E,F在直线AB的同侧时(如图①所示),试说明∠BOE=2∠COF.
(2)当点C与点E,F在直线AB的两侧时(如图②所示),(1)中的结论是否仍然成立?请给出你的结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
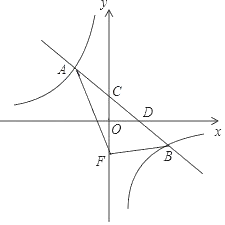
【题目】在平面直角坐标系中,一次函数y=﹣![]() x+b的图象与反比例函数y=
x+b的图象与反比例函数y=![]() (k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(1)求一次函数和反比例函数解析式.
(2)若将点C沿y轴向下平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
(3)根据图象,直接写出不等式﹣![]() x+b>
x+b>![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
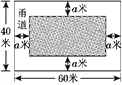
【题目】如图①,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上,修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的甬道,设甬道的宽为a米.
 ①
①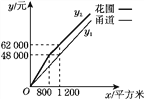 ②
②
(1)用含a的式子表示花圃的面积;
(2)如果甬道所占面积是整个长方形空地面积的![]() ,求此时甬道的宽;
,求此时甬道的宽;
(3)已知某园林公司修建甬道、花圃的造价y1(元)、y2(元)与修建面积x(平方米)之间的函数关系如图②所示.如果学校决定由该公司承建此项目,并要求修建的甬道宽不少于2米且不超过10米,那么甬道的宽为多少米时,修建的甬道和花圃的总造价最低?最低总造价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
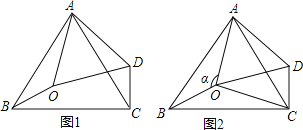
【题目】如图1,在△ABC中,∠BAC=60°,点0是△ABC内一点,△AB0![]() △ACD,连接OD.
△ACD,连接OD.
(1)求证△AOD为等边三角形。
(2)如图2,连接OC,若∠BOC=130°,∠AOB=![]() .
.
①求∠OCD的度数
②当△OCD是等腰三角形时,求∠![]() 的度数
的度数
 、
、
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com