
【题目】如图,∠AOB的边OA上有一动点P,从距离O点18cm的点M处出发,沿线段MO,射线OB运动,速度为2cm/s;动点Q从点O出发,沿射线OB运动,速度为1cm/s.P、Q同时出发,设运动时间是t(s).
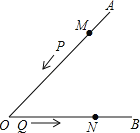
(1)当点P在MO上运动时,PO= cm (用含t的代数式表示);
(2)当点P在MO上运动时,t为何值,能使OP=OQ?
(3)若点Q运动到距离O点16cm的点N处停止,在点Q停止运动前,点P能否追上点Q?如果能,求出t的值;如果不能,请说出理由.
【答案】(1)(18﹣2t);(2)t=6时,能使OP=OQ;(3)点P追上点Q需要18s,此时点Q已经停止运动.
【解析】
试题分析:(1)利用P点运动速度以及OM的距离进而得出答案;
(2)利用OP=OQ列出方程求出即可;
(3)利用假设追上时,求出所用时间,进而得出答案.
解:(1)∵P点运动速度为2cm/s,MO=18cm,
∴当点P在MO上运动时,PO=(18﹣2t)cm,
故答案为:(18﹣2t);
(2)当OP=OQ时,则有18﹣2t=t,
解这个方程,得t=6,
即t=6时,能使OP=OQ;
(3)不能.理由如下:
设当t秒时点P追上点Q,则2t=t+18,
解这个方程,得t=18,
即点P追上点Q需要18s,此时点Q已经停止运动.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
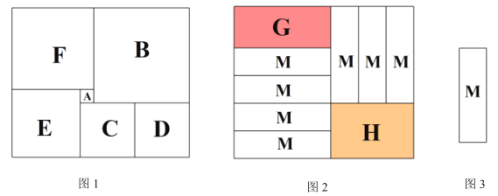
【题目】如图1,有一个长方形被分割成了6个大小不同的正方形,其中最小正方形的边长是3,则该长方形长是___________;将同一个长方形作如图2分割,分割成左上角的长方形G、右下角的长方形H以及7张长宽相同的小长方形M(小长方形M如图3所示),当长方形G与长方形H的周长相等时,小长方形M的宽是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
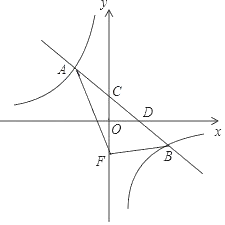
【题目】在平面直角坐标系中,一次函数y=﹣![]() x+b的图象与反比例函数y=
x+b的图象与反比例函数y=![]() (k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(1)求一次函数和反比例函数解析式.
(2)若将点C沿y轴向下平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
(3)根据图象,直接写出不等式﹣![]() x+b>
x+b>![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
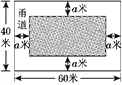
【题目】如图①,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上,修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的甬道,设甬道的宽为a米.
 ①
①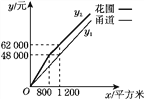 ②
②
(1)用含a的式子表示花圃的面积;
(2)如果甬道所占面积是整个长方形空地面积的![]() ,求此时甬道的宽;
,求此时甬道的宽;
(3)已知某园林公司修建甬道、花圃的造价y1(元)、y2(元)与修建面积x(平方米)之间的函数关系如图②所示.如果学校决定由该公司承建此项目,并要求修建的甬道宽不少于2米且不超过10米,那么甬道的宽为多少米时,修建的甬道和花圃的总造价最低?最低总造价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某淘宝店家为迎接“双十一”抢购活动,在甲批发市场以每件a元的价格进了40件童装,又在乙批发市场以每件b元(a>b)的价格进了同样的60件童装.如果店家以每件![]() 元的价格卖出这款童装,卖完后,这家商店( )
元的价格卖出这款童装,卖完后,这家商店( )
A.盈利了B.亏损了
C.不赢不亏D.盈亏不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)某中学初二年级抽取部分学生进行跳绳测试.并规定:每分钟跳90次以下的为不及格;每分钟跳90~99次的为及格;每分钟跳100~109次的为中等;每分钟跳110~119次的为良好;每分钟跳120次及以上的为优秀.测试结果整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:

(1)参加这次跳绳测试的共有 人;
(2)补全条形统计图;
(3)在扇形统计图中,“中等”部分所对应的圆心角的度数是 ;
(4)如果该校初二年级的总人数是480人,根据此统计数据,请你估算该校初二年级跳绳成绩为“优秀”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,BD是矩形ABCD的对角线,![]() ,
,![]() .将
.将![]() 沿射线BD方向平移到
沿射线BD方向平移到![]() 的位置,连接
的位置,连接![]() ,
,![]() ,
,![]() ,
,![]() ,如图2.
,如图2.
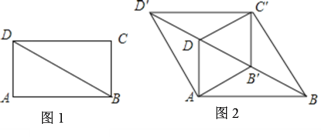
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 是菱形,请说明理由;
是菱形,请说明理由;
(3)在(2)的条件下,将四边形![]() 沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
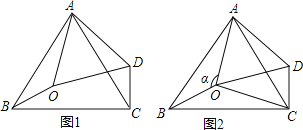
【题目】如图1,在△ABC中,∠BAC=60°,点0是△ABC内一点,△AB0![]() △ACD,连接OD.
△ACD,连接OD.
(1)求证△AOD为等边三角形。
(2)如图2,连接OC,若∠BOC=130°,∠AOB=![]() .
.
①求∠OCD的度数
②当△OCD是等腰三角形时,求∠![]() 的度数
的度数
 、
、
查看答案和解析>>
科目:初中数学 来源: 题型:
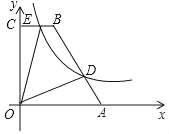
【题目】如图,在四边形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且![]() ,双曲线y=
,双曲线y=![]() (k>0)经过点D,交BC于点E
(k>0)经过点D,交BC于点E
(1)求双曲线的解析式;
(2)求四边形ODBE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com