
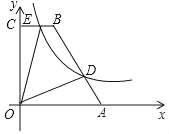
【题目】如图,在四边形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且![]() ,双曲线y=
,双曲线y=![]() (k>0)经过点D,交BC于点E
(k>0)经过点D,交BC于点E
(1)求双曲线的解析式;
(2)求四边形ODBE的面积.
【答案】(1)y=![]() (2)12
(2)12
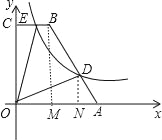
【解析】分析:(1)作BM⊥x轴于M,作DN⊥x轴于N,利用点A,B的坐标得到BC=OM=2,BM=OC=6,AM=3,再证明△ADN∽△ABM,利用相似比可计算出DN=2,AN=1,则ON=OA-AN=4,得到D点坐标为(4,2),然后把D点坐标代入y=![]() 中求出k的值即可得到反比例函数解析式;
中求出k的值即可得到反比例函数解析式;
(2)根据反比例函数k的几何意义和S四边形ODBE=S梯形OABC-S△OCE-S△OAD进行计算.
详解:(1)作BM⊥x轴于M,作DN⊥x轴于N,如图,
∵点A,B的坐标分别为(5,0),(2,6),
∴BC=OM=2,BM=OC=6,AM=3,
∵DN∥BM,
∴△ADN∽△ABM,
∴![]() ,即
,即![]() ,
,
∴DN=2,AN=1,
∴ON=OA﹣AN=4,
∴D点坐标为(4,2),
把D(4,2)代入y=![]() 得k=2×4=8,
得k=2×4=8,
∴反比例函数解析式为y=![]() ;
;
(2)S四边形ODBE=S梯形OABC﹣S△OCE﹣S△OAD
=![]() ×(2+5)×6﹣
×(2+5)×6﹣![]() ×|8|﹣
×|8|﹣![]() ×5×2
×5×2
=12.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
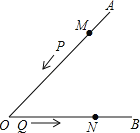
【题目】如图,∠AOB的边OA上有一动点P,从距离O点18cm的点M处出发,沿线段MO,射线OB运动,速度为2cm/s;动点Q从点O出发,沿射线OB运动,速度为1cm/s.P、Q同时出发,设运动时间是t(s).
(1)当点P在MO上运动时,PO= cm (用含t的代数式表示);
(2)当点P在MO上运动时,t为何值,能使OP=OQ?
(3)若点Q运动到距离O点16cm的点N处停止,在点Q停止运动前,点P能否追上点Q?如果能,求出t的值;如果不能,请说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连结BO,若S△AOB=4.

(1)求该反比例函数的解析式和直线AB的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·漳州)(满分8分)漳州市某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:

(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有_ ▲ 人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题。
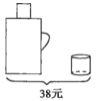
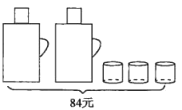
(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯.若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (1≤x≤8)的图象记为曲线C1,将C1沿y轴翻折,得到曲线C2,直线y=-x+b 与C1 ,C2一共只有两个公共点,则b的取值范围是______________________.
(1≤x≤8)的图象记为曲线C1,将C1沿y轴翻折,得到曲线C2,直线y=-x+b 与C1 ,C2一共只有两个公共点,则b的取值范围是______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
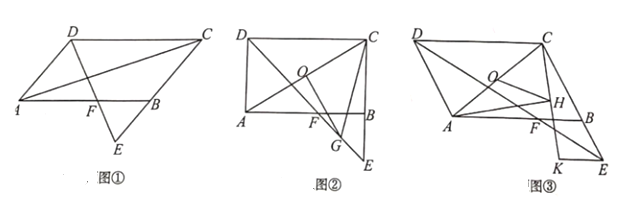
【题目】在ABCD中,∠ADC的平分线交直线BC于点E,交直线AB于点F.
(1)如图①,证明:BE=BF.
(2)如图②,若∠ADC=90°,O为AC的中点,G为EF的中点,试探究OG与AC的位置关系,并说明理由.
(3)如图③,若∠ADC=60°,过点E作DC的平行线,并在其上取一点K(与点F位于直线BC的同侧),使EK=BF,连接CK,H为CK的中点,试探究线段OH与HA之间的数量关系,并对结论给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com