
【题目】如下图,将边长为 9cm 的正方形纸片 ABCD 折叠,使得点 A 落在边 CD 上的 E 点,折痕为 MN.若 CE 的长为 6cm,则 MN 的长为_____cm.

 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连结BO,若S△AOB=4.

(1)求该反比例函数的解析式和直线AB的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (1≤x≤8)的图象记为曲线C1,将C1沿y轴翻折,得到曲线C2,直线y=-x+b 与C1 ,C2一共只有两个公共点,则b的取值范围是______________________.
(1≤x≤8)的图象记为曲线C1,将C1沿y轴翻折,得到曲线C2,直线y=-x+b 与C1 ,C2一共只有两个公共点,则b的取值范围是______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
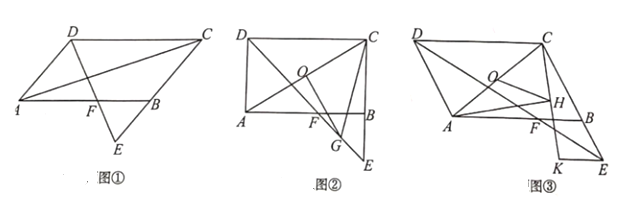
【题目】在ABCD中,∠ADC的平分线交直线BC于点E,交直线AB于点F.
(1)如图①,证明:BE=BF.
(2)如图②,若∠ADC=90°,O为AC的中点,G为EF的中点,试探究OG与AC的位置关系,并说明理由.
(3)如图③,若∠ADC=60°,过点E作DC的平行线,并在其上取一点K(与点F位于直线BC的同侧),使EK=BF,连接CK,H为CK的中点,试探究线段OH与HA之间的数量关系,并对结论给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某月的日历表,在此日历表上可以用一个矩形圈出3×3个位置的9个数(如6,7,8,13,14,15,20,21,22).若圈出的9个数中,最大数与最小数的和为42,则这9个数的和为( )

A. 69 B. 84 C. 189 D. 207
查看答案和解析>>
科目:初中数学 来源: 题型:
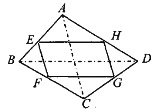
【题目】如图,四边形 ABCD 中,E、F、G、H 分别为各边的中点,顺次连 结 E、F、G、H,把四边形 EFGH 称为中点四边形.连结 AC、BD,容易证明:中点 四边形 EFGH 一定是平行四边形.
(1)如果改变原四边形 ABCD 的形状,那么中点四边形的形状也随之改变,通过探索 可以发现:当四边形 AB CD 的对角线满足 AC=BD 时,四边形 EFGH 为菱形;当四边形ABCD 的对角线满足 时,四边形 EFGH 为矩形;当四边形 ABCD 的对角线满足 时,四边形 EFGH 为正方形.
(2)试证明:S△AEH+S△CFG= ![]() S□ ABCD
S□ ABCD
(3)利用(2)的结论计算:如果四边形 ABCD 的面积为 2012, 那么中点四边形 EFGH 的面积是 (直接将结果填在 横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C,D在线段AB上,M、N分别是AC、BD的中点,若AB=20,CD=4,
(1)求MN的长.
(2)若AB=a,CD=b,请用含有a、b的代数式表示出MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=﹣x+2与x轴、y轴分别交于点A、点C,抛物线经过点A、点C,且与x轴的另一个交点为B(﹣1,0).
(1)求抛物线的解析式;
(2)点D为第一象限内抛物线上的一动点.
①如图1,若CD=AD,求点D的坐标;
②如图2,BD与AC交于点E,求S△CDE:S△CBE的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com