
【题目】“一带一路”倡议提出3年多来,交通、通信、能源等各项相关建设取得积极进展,也为增进各国民众福祉提供了新的发展机遇.如图,是“一带一路”沿线部分国家的通信设施现状统计图.观察图,请回答下列问题:
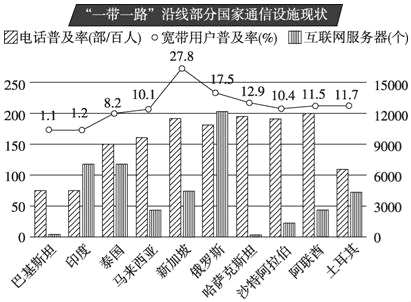
(1)在这10个国家中,互联网服务器拥有个数最多的国家是 ;
(2)在这10个国家中,每100人拥有电话数量最接近150部的国家是 ;
(3)在这10个国家中,宽带用户普及率最高的国家是 ,普及率为 ;
(4)在这10个国家中,宽带用户普及率的中位数是 .
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】(11·漳州)(满分8分)漳州市某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:

(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有_ ▲ 人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
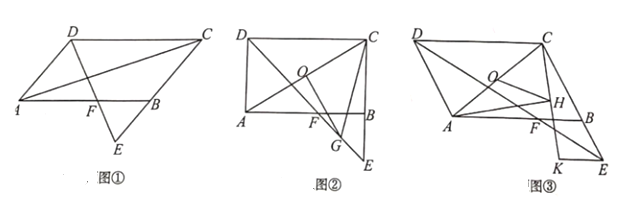
【题目】在ABCD中,∠ADC的平分线交直线BC于点E,交直线AB于点F.
(1)如图①,证明:BE=BF.
(2)如图②,若∠ADC=90°,O为AC的中点,G为EF的中点,试探究OG与AC的位置关系,并说明理由.
(3)如图③,若∠ADC=60°,过点E作DC的平行线,并在其上取一点K(与点F位于直线BC的同侧),使EK=BF,连接CK,H为CK的中点,试探究线段OH与HA之间的数量关系,并对结论给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
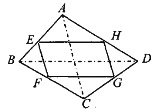
【题目】如图,四边形 ABCD 中,E、F、G、H 分别为各边的中点,顺次连 结 E、F、G、H,把四边形 EFGH 称为中点四边形.连结 AC、BD,容易证明:中点 四边形 EFGH 一定是平行四边形.
(1)如果改变原四边形 ABCD 的形状,那么中点四边形的形状也随之改变,通过探索 可以发现:当四边形 AB CD 的对角线满足 AC=BD 时,四边形 EFGH 为菱形;当四边形ABCD 的对角线满足 时,四边形 EFGH 为矩形;当四边形 ABCD 的对角线满足 时,四边形 EFGH 为正方形.
(2)试证明:S△AEH+S△CFG= ![]() S□ ABCD
S□ ABCD
(3)利用(2)的结论计算:如果四边形 ABCD 的面积为 2012, 那么中点四边形 EFGH 的面积是 (直接将结果填在 横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C,D在线段AB上,M、N分别是AC、BD的中点,若AB=20,CD=4,
(1)求MN的长.
(2)若AB=a,CD=b,请用含有a、b的代数式表示出MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE,CF交于点D,则下列结论中不正确的是( )

A. △ABE≌△ACF B. 点D在∠BAC的平分线上
C. △BDF≌△CDE D. D是BE的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三位自然数m,将它任意两个数位上的数字对调后得一个首位不为0 的新三位自然数 m’( m’可以与m相同),记m’=![]() ,在 m’ 所有的可能情况中,当|a+2b-c| 最小时,我们称此时的m’ 是m 的“幸福美满数”,并规定K (m) = a2 +2b2 -c2.例如:318按上述方法可得新数有:381、813 、138 ;因为|3+2
,在 m’ 所有的可能情况中,当|a+2b-c| 最小时,我们称此时的m’ 是m 的“幸福美满数”,并规定K (m) = a2 +2b2 -c2.例如:318按上述方法可得新数有:381、813 、138 ;因为|3+2![]() 8-1|= 18 ,|8+ 2
8-1|= 18 ,|8+ 2![]() 1-3|=7,|1 +2
1-3|=7,|1 +2![]() 3-8|=1,1< 7<18 ,所以138 是318的“幸福美满数”,K(318)=|12+2
3-8|=1,1< 7<18 ,所以138 是318的“幸福美满数”,K(318)=|12+2![]() 32-82|=-45.
32-82|=-45.
(1)若三位自然数t的百位上的数字与十位上的数字都为n(1≤n ≤ 9 ,n为自然数),个位上的数字为0 ,求证:K (t )= 0;
(2)设三位自然数s=100+10x + y(1≤ x ≤ 9,1≤y≤9, ,x y 为自然数) ,且x<y .交换其个位与十位上的数字得到新数s’,若19s+8s’=3888,那么我们称s为“梦
想成真数”,求所有“梦想成真数”中K (s )的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com