
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,过点
上,过点![]() 作
作![]() 的切线
的切线![]() .
.

![]() 求证:
求证:![]() ;
;
![]() 延长
延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() 的半径为
的半径为![]() ,
,![]() ,求
,求![]() 的外接圆的半径.
的外接圆的半径.
【答案】(1)详见解析;(2)![]() 的外接圆的半径为:
的外接圆的半径为:![]() .
.
【解析】
(1)连接OC,由∠ABC+∠BAC=90°及CM是⊙O的切线得出∠ACM+∠ACO=90°,再利用∠BAC=∠ACO,即可得出结论,(2)证明△AEC是直角三角形,即可得△AEC的外接圆的直径是AC,再证得△ABC∽△CDE,根据相似三角形的性质求得BC的长,利用勾股定理求出AC的长,即可求得△ACE的外接圆的半径.
![]() 证明:如图,连接
证明:如图,连接![]() ,
,
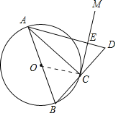
∵![]() 为
为![]() 的直径,
的直径,
∴![]() ,
,
∴![]() ,
,
又∵![]() 是
是![]() 的切线,
的切线,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 解:∵
解:∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() 是直角三角形,
是直角三角形,
∴![]() 的外接圆的直径是
的外接圆的直径是![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() 的半径为
的半径为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的外接圆的半径为
的外接圆的半径为![]() 的一半,故
的一半,故![]() 的外接圆的半径为:
的外接圆的半径为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数![]() 的图象上.若点A的坐标为(-2,-2),则k的值为 。
的图象上.若点A的坐标为(-2,-2),则k的值为 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条河的北岸有两个目标M、N,现在位于它的对岸设定两个观测点A、B.已知AB∥MN,在A点测得∠MAB=60°,在B点测得∠MBA=45°,AB=600米.
(1)求点M到AB的距离;(结果保留根号)
(2)在B点又测得∠NBA=53°,求MN的长.(结果精确到1米)
(参考数据:![]() ≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)
≈1.732,sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“绿色出行”的号召,小王上班由自驾车改为乘坐公交车.已知小王家距离上班地点![]() ,他乘坐公交车平均每小时行驶的路程比他自驾车平均每小时行驶的路程的
,他乘坐公交车平均每小时行驶的路程比他自驾车平均每小时行驶的路程的![]() 倍还多
倍还多![]() .他从家出发到上班地点,乘公交车所用的时间是自驾车所用时间的
.他从家出发到上班地点,乘公交车所用的时间是自驾车所用时间的![]() .
.
(1)小王用自驾车上班平均每小时行驶多少千米?
(2)上周五,小王上班时先步行了![]() ,然后乘公交车前往,共用
,然后乘公交车前往,共用![]() 小时到达.求他步行的速度.
小时到达.求他步行的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰直角三角形![]() 中,
中,![]() 、
、![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 、
、![]() 的中点,点
的中点,点![]() 为斜边
为斜边![]() 所在直线上一动点,且三角形
所在直线上一动点,且三角形![]() 为等腰直角三角形(
为等腰直角三角形(![]() ,
,![]() 、
、![]() 、
、![]() 呈逆时针).
呈逆时针).
![]() 如图
如图![]() 点
点![]() 在边
在边![]() 上,判断
上,判断![]() 和
和![]() 的数量和位置关系,请直接写出你的结论.
的数量和位置关系,请直接写出你的结论.
![]() 如图
如图![]() 点
点![]() 在
在![]() 点左侧时;如图
点左侧时;如图![]() ,点
,点![]() 在
在![]() 点右侧.其他条件不变,
点右侧.其他条件不变,![]() 中结论是否仍然成立,并选择图
中结论是否仍然成立,并选择图![]() 或图
或图![]() 的一种情况来说明理由.
的一种情况来说明理由.
![]() 在图
在图![]() 中若
中若![]() ,连接
,连接![]() ,请猜测
,请猜测![]() 与
与![]() 的数量关系,即
的数量关系,即![]() ________
________![]() .(用含
.(用含![]() 的三角函数的式子表示)
的三角函数的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE=α,直线AE与BD交于点F.
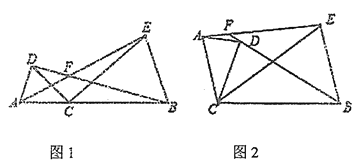
(1)如图1所示,
①求证AE= BD
②求∠AFB (用含α的代数式表示)
(2)将图1中的△ACD绕点C顺时针旋转某个角度(交点F至少在BD、AE中的一条线段上),得到如图2所示的图形,若∠AFB= 150°,请直接写出此时对应的α的大小(不用证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y1=kx+1(k<0)与直线y2=mx(m>0)的交点坐标为(![]() ,
,![]() m),则不等式组mx﹣2<kx+1<mx的解集为( )
m),则不等式组mx﹣2<kx+1<mx的解集为( )
A. x>![]() B.
B. ![]() <x<
<x<![]() C. x<
C. x<![]() D. 0<x<
D. 0<x<![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太极揉推器是一种常见的健身器材.基本结构包括支架和转盘,数学兴趣小组的同学对某太极揉推器的部分数据进行了测量:如图,立柱AB的长为125cm,支架CD、CE的长分别为60cm、40cm,支点C到立柱顶点B的距离为25cm.支架CD,CE与立柱AB的夹角∠BCD=∠BCE=45°,转盘的直径FG=MN=60cm,D,E分别是FG,MN的中点,且CD⊥FG,CE⊥MN,则两个转盘的最低点F,N距离地面的高度差为_____cm.(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com