
【题目】今年某区为绿化行车道,计划购买甲、乙两种树苗共计n棵.设购买甲种树苗x棵,有关甲、乙两种树苗的信息如图所示.
(1)当n=500时,
①根据信息填表(用含x的式子表示);
树苗类型 | 甲种树苗 | 乙种树苗 |
购买树苗数量(单位:棵) | x | |
购买树苗的总费用(单位:元) |
②如果购买甲、乙两种树苗共用去25 600元,那么甲、乙两种树苗各购买了多少棵?
(2)要使这批树苗的成活率不低于92%,且使购买这两种树苗的总费用为26 000元,求n的最大值.

【答案】(1) ①500-x 50x 80(500-x) ②甲种树苗购买了480棵,乙种树苗购买了20棵 (2) 418.
【解析】试题分析:(1)设甲种树苗的数量为x棵,则乙种树苗的数量为500-x棵,根据购买甲、乙两种树苗共用25600元可列方程求解即可;
(2)根据这批树苗的成活率不低于92%可列出不等式求解.
试题解析:解:(1)①500-x,50x,80(500-x);
②50x+80(500-x)=25 600,解得:x=480,500-x=20.
答:甲种树苗购买了480棵,乙种树苗购买了20棵.
(2)依题意,得:90%x+95%(n-x)≥92%×n,解得:x≤![]() n.
n.
又50x+80(n-x)=26 000,解得:x=![]() ,
,
∴![]() ≤
≤![]() n,∴n≤
n,∴n≤![]() .
.
∵n为正整数,∴n的最大值为419.
∵当n=419时,x=![]() =
=![]() 不是整数;
不是整数;
当n=418时,x=![]() =248是整数,∴n=418.
=248是整数,∴n=418.


科目:初中数学 来源: 题型:
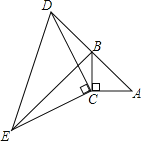
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
(1)求证:△ACD≌△BCE;
(2)若AC=3,求BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程:
(1) x2﹣5x﹣6=0;
(2) (1﹣x)2﹣1=![]() ;
;
(3) 8x(x+2)=3x+6;
(4)(y+![]() )(y-
)(y-![]() )=20.
)=20.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及S四边形ABDC.
(2)在y轴上是否存在一点Q,连接QA,QB,使S△QAB=S四边形ABDC?若存在这样一点,求出点Q的坐标;若不存在,试说明理由.
(3)如图②,点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合),给出下列结论:①![]() 的值不变,②
的值不变,②![]() 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)例:代数式(a+b)2表示a、b两数和的平方.仿照上例填空:
代数式a2﹣b2表示_____.
代数式(a+b)(a﹣b)表示_____.
(2)试计算a、b取不同数值时,a2﹣b2及(a+b)(a﹣b)的植,填入下表:

(3)请你再任意给a、b各取一个数值,并计算a2﹣b2及(a+b)(a﹣b)的植:
当a=_____,b=_____时,a2﹣b2=_____,(a+b)(a﹣b)=_____.
(4)我的发现:_____.
(5)用你发现的规律计算:78.352﹣21.652.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D.

(1)∠ECD和∠EDC相等吗?说明理由.
(2)OC和OD相等吗?说明理由.
(3)OE是线段CD的垂直平分线吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张阳从家里跑步去体育场,在那里锻炼了一会儿后,又走到文具店去买笔,然后走回家,如图是张阳离家的距离与时间的关系图象.
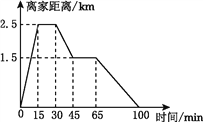
根据图象回答下列问题:
(1)体育场离张阳家多少千米?
(2)体育场离文具店多少千米?张阳在文具店逗留了多长时间?
(3)张阳从文具店到家的速度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com