
【题目】小明在学习过程中遇到这样一个问题:如图1,在△ABC中,CA=CB,E是CD上一点,且ED=EB, ∠DEB=∠ACB,连接AD,探究∠ADC与∠DCB之间的数量关系.小明发现,∠ACD=∠CBE,CA=CB,因此可以通过作∠CAF=∠BCE交CD于点F构造全等,经过推理论证解决问题.
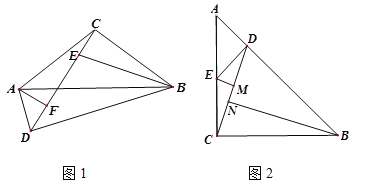
(1)按照小明思考问题的方法,解决问题;
(2)如图2,∠ACB=90,CA=CB,D是AB上一点,过点D作DE⊥AB交AC于点E,过点E作EM⊥CD于点M,BN⊥CD于点N,探究EM,BN,CD之间的数量关系.
【答案】(1)∠DCB=2∠ADC,证明详见解析;(2)BN= CD+EM,理由详见解析.
【解析】
(1)∠DCB=2∠ADC,作∠CAF=∠BCE交CD于点F,证明△ACF≌△CBE,根据全等三角形的性质可得AF=CE,CF=BE,∠AFC=∠DCB,再证得AF=DF,根据等腰三角形的性质可得∠ADF=∠DAF,由三角形外角的性质即可证得结论;(2)BN= CD+EM,过点A作AH⊥CD交CD的延长线于点H(如图2),先证得Rt△ACH≌Rt△CBN,根据全等三角形的性质可得CH=BN,再证得Rt△ADH≌Rt△DEM,根据全等三角形的性质可得EM=DH,由BN= CD+DH= CD+EM.即可证得结论.
(1)∠DCB=2∠ADC,理由如下,
如图1,作∠CAF=∠BCE交CD于点F,

∵∠DEB=∠EBC+∠ECB,∠ACB=∠ACF+∠ECB,∠DEB=∠ACB,
∴∠ACF=∠CBE,
在△ACF和△CBE中,
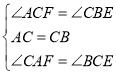
∴△ACF≌△CBE,
∴AF=CE,CF=BE,∠AFC=∠DCB,
∵DE=EB,
∴DE=CF,
∴DF=CE,
∵AF=CE,
∴AF=DF,
∴∠ADF=∠DAF,
∴∠AFC=∠ADF+∠DAF=2∠ADC,
∵∠AFC=∠DCB,
∴∠DCB=2∠ADC.
(2)BN= CD+EM,理由如下:
过点A作AH⊥CD交CD的延长线于点H(如图2),
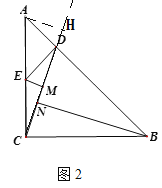
∵AH⊥CD,BN⊥CD,
∴∠AHC=∠CNB=90°,
∴∠CBN+∠NCB=90°,
∵∠ACH+∠NCB=90°,
∴∠CBN=∠ACH,
在Rt△ACH和Rt△CBN中,
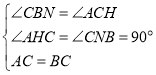 ,
,
∴Rt△ACH≌Rt△CBN,
∴CH=BN,
∵∠ACB=90,CA=CB,
∴∠EDA=45°,
∵DE⊥AB,
∴△AED为等腰直角三角形,
∴AD=DE,
∵AH⊥CD,EM⊥CD,
∴∠AHD=∠DME=90°,
∴∠DAH+∠ADH=90°,
∵∠ADH+∠EDM=90°,
∴∠DAH=∠EDM,
在Rt△ADH和Rt△DEM中,
 ,
,
∴Rt△ADH≌Rt△DEM,
∴EM=DH,
∵CH=CD+DH,CH=BN,
∴BN= CD+DH= CD+EM.


科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,重庆仙女山风景区7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 单位:万人 | +1.2 | +0.4 | +0.8 | ﹣0.4 | ﹣0.8 | +0.2 | ﹣1.2 |
(1)若9月30日的游客人数记为a,请用含a的式子表示10月5日的游客人数: 万人.
(2)判断七天内游客人数最多的是 日,最少的是 日.
(3)以9月30日的游客人数为0点,用折线统计图表示这7天的游客人数情况:人数变化(万人)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
![]() “明天降雨的概率是
“明天降雨的概率是![]() ”表示明天有半天都在降雨;
”表示明天有半天都在降雨;
![]() 无理数是开方开不尽的数;
无理数是开方开不尽的数;
![]() 若
若![]() 为实数,则
为实数,则![]() 是不可能事件;
是不可能事件;
![]() 的平方根是
的平方根是![]() ,用式子表示是
,用式子表示是![]() ;
;
![]() 某班的5位同学在向“创建图书角”捐款活动中,捐款数如下(单位:元):8,3,8,2,4,那么这组数据的众数是8,中位数是4,平均数是5.其中正确的个数有( )
某班的5位同学在向“创建图书角”捐款活动中,捐款数如下(单位:元):8,3,8,2,4,那么这组数据的众数是8,中位数是4,平均数是5.其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校的教室A位于工地O的正西方向,且OA=200米,一部拖拉机从O点出发,以每秒5米的速度沿北偏西53°方向行驶,设拖拉机的噪声污染半径为130米,试问教室A是否在拖拉机的噪声污染范围内,若不在,请说明理由;若在,求出教室A受污染的时间有几秒.(已知:sin53°≈0.80,sin37°≈0.60,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片 ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、 AC于点E、G.连接GF.则下列结论错误的是( )
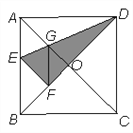
A. ∠AGD=112.5° B. 四边形AEFG是菱形 C. tan∠AED=2 D. BE=2OG
查看答案和解析>>
科目:初中数学 来源: 题型:
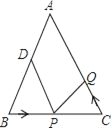
【题目】如图△ABC,AB=AC=24厘米,∠B=∠C,BC=16厘米,点D为AB的中点.点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为_____ 厘米/秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师为学校新年联欢会购买奖品,在某文具用品店购买明信片,每一张明信片的价格是8元,在结算时发现,如果再多买5张,就可以享受到打九折的优惠,总价格反而减少8元,为了能享受优惠,王老师比原计划多购买了5张明信片;
(1)王老师实际购买多少张明信片?一共花了多少钱?
(2)文具店开展元旦优惠活动:从即日起,在一周内,凭购物小票,累计购物超过500元,超过部分可以享受八折的优惠.王老师想了一想,又为学校购买了一定数量的笔记本,享受了八折优惠,这样,两次一共节省了36元,王老师购买笔记本实际花了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用火柴棒摆出一列正方形图案,第①个图案用了 4 根,第②个图案用了 12 根,第③个图案用了 24 根,按照这种方式摆下去,摆出第⑥个图案用火柴棒的根数是( )

A. 84 B. 81 C. 78 D. 76
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com