
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:
①a+b+c<0;②a﹣b+c>1;③abc>0;④4a﹣2b+c<0;
其中正确的结论是 .
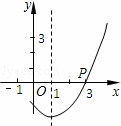
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
2012伦敦奥运会主会场的座席数是91000个,这个数用科学记数法表示为( )
A. 0.91×105 B. 9.1×104 C. 91×103 D. 9.1×103
查看答案和解析>>
科目:初中数学 来源: 题型:
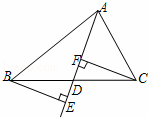
如图,△ABC中,已知BE⊥AD,CF⊥AD,且BE=CF.
(1)证明:△BDE≌△CDF;
(2)给△ABC添加一个条件 ,使AD平分∠BAC.
(直接填写添加的条件,不需要证明.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com