
我们知道,经过原点的抛物线解析式可以是 。
。
(1)对于这样的抛物线:
当顶点坐标为(1,1)时,a= ;
当顶点坐标为(m,m),m≠0时,a 与m之间的关系式是 ;
(2)继续探究,如果b≠0,且过原点的抛物线顶点在直线 上,请用含k的代数式表示b;
上,请用含k的代数式表示b;
(3)现有一组过原点的抛物线,顶点A1,A2,…,An在直线 上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,B3,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过点Dn,求所有满足条件的正方形边长。
上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,B3,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过点Dn,求所有满足条件的正方形边长。
(1)-1;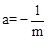 (2)
(2)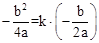 (3)3,6,9
(3)3,6,9
【解析】解:(1)-1;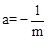 。
。
(2)∵过原点的抛物线顶点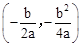 在直线
在直线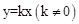 上,∴
上,∴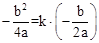 。
。
∵b≠0,∴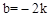 。
。
(3)由(2)知,顶点在直线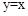 上,横坐标依次为1,2,…,n(n为正整数,且n≤12)的抛物线为:
上,横坐标依次为1,2,…,n(n为正整数,且n≤12)的抛物线为: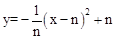 ,即
,即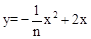 。
。
对于顶点在在直线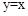 上的一点A m(m,m)(m为正整数,且m≤n),依题意,作的正方形AmBmCmDm边长为m,点Dm坐标为(2 m,m),
上的一点A m(m,m)(m为正整数,且m≤n),依题意,作的正方形AmBmCmDm边长为m,点Dm坐标为(2 m,m),
若点Dm在某一抛物线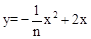 上,则
上,则
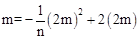 ,化简,得
,化简,得 。
。
∵m,n为正整数,且m≤n≤12,∴n=4,8,12,m=3,6,9。
∴所有满足条件的正方形边长为3,6,9。
(1)当顶点坐标为(1,1)时,由抛物线顶点坐标公式,有 ,即
,即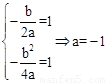 。
。
当顶点坐标为(m,m),m≠0时,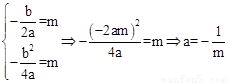 。
。
(2)根据点在直线上,点的坐标满足方程的关系,将抛物线顶点坐标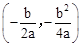 代入
代入 ,
,
化简即可用含k的代数式表示b。
由于抛物线与直线只有一个公共点,意味着联立解析式后得到的一元二次方程,其根的判别式等于0,由此可求出m的值和D点坐标。
(3)将依题意,作的正方形AmBmCmDm边长为m,点Dm坐标为(2 m,m),将(2 m,m)代入抛物线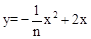 求出m,n的关系,即可求解。
求出m,n的关系,即可求解。


科目:初中数学 来源: 题型:
| 1 |
| m |
| 1 |
| m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:福州 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2013年福建省福州市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com