
【题目】如图,![]() 点的初始位置位于数轴上表示
点的初始位置位于数轴上表示![]() 的点,现对
的点,现对![]() 点做如下移动:第
点做如下移动:第![]() 次向左移动
次向左移动![]() 个单位长度至
个单位长度至![]() 点,第
点,第![]() 次从
次从![]() 点向右移动
点向右移动![]() 个单位长度至
个单位长度至![]() 点,第
点,第![]() 次从
次从![]() 点向左移动
点向左移动![]() 个单位长度至
个单位长度至![]() 点,第
点,第![]() 次从
次从![]() 点向右移动
点向右移动![]() 个单位长度至
个单位长度至![]() 点,…,依此类推。这样第_____次移动到的点到原点的距离为
点,…,依此类推。这样第_____次移动到的点到原点的距离为![]() .
.
![]()
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数![]() 的图象经过点A(1,4)和点B.过点A作AC⊥x轴,垂足为点C,过点B作BD⊥y轴,垂足为点D,连结AB、BC、DC、DA.点B的横坐标为a(a>1)
的图象经过点A(1,4)和点B.过点A作AC⊥x轴,垂足为点C,过点B作BD⊥y轴,垂足为点D,连结AB、BC、DC、DA.点B的横坐标为a(a>1)
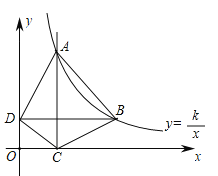
(1)求k的值
(2)若△ABD的面积为4;
①求点B的坐标,
②在平面内存在点E,使得以点A、B、C、E为顶点的四边形是平行四边形,直接写出符合条件的所有点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为( )
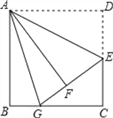
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
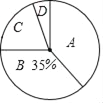
【题目】2017年4月15日至5月15日,某市约8万名初三毕业生参加了中考体育测试,为了了解今年初三毕业生的体育成绩,从某校随机抽取了60名学生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
等级 | 成绩(分) | 频数(人数) | 频率 |
A | 27~30 | 24 | 0.4 |
B | 23~26 | m | x |
C | 19~22 | n | y |
D | 18及18以下 | 3 | 0.05 |
合计 | 60 | 1.00 |
请你根据以上图表提供的信息,解答下列问题:
(1)m= ,n= ,x= ,y= ;
(2)在扇形图中,B等级所对应的圆心角是 度;
(3)请你估计某市这8万名初三毕业生成绩等级达到优秀和良好的大约有多少人?
(4)初三(1)班的甲、乙、丙、丁四人的成绩均为A,现决定从这四名同学中选两名参加学校组织的体育活动,直接写出恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嫦娥四号探测器于2019年1月3日,成功着陆在月球背面,通过“鹊桥”中继星传回了世界第一张近距离拍摄的月背影像图,开启了人类月球探测新篇章.当中继星成功运行于地月拉格朗日L2点时,它距离地球约1500000km.用科学记数法表示数1500000为( )

A. 15×105 B. 1.5×106 C. 0.15×107 D. 1.5×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示.
(1)求乙车离开A城的距离y关于t的函数解析式;
(2)求乙车的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级甲、乙两班举行电脑汉字输入比赛,两个班能参加比赛的学生每分钟输入汉字的个数,经统计和计算后结果如下表:

有一位同学根据上面表格得出如下结论:
①甲、乙两班学生的平均水平相同;②乙班优秀人数比甲班优秀人数多(每分钟输入汉字达150个以上为优秀);③甲班学生比赛成绩的波动比乙班学生比赛成绩的波动大.
上述结论正确的是_______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
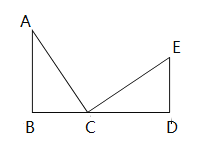
【题目】如图,在△ABC中,∠B=90°,点B、C、D在同一直线上,△ABC≌△CDE,且∠B=∠D,∠BAC=∠DCE.
(1)试说明BD=AB+ED;
(2)若∠CED=2∠BAC,求∠CED的度数;
(3)连接AE,则△ACE是怎样的三角形?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com