D
分析:根据方程x
2-ax+a
2-3=0至少有一个正根,则方程一定有两个实数根,即△≥0,关于x的方程x
2-ax+a
2-3=0至少有一个正根?(1)当方程只有一个根,且为正根,(2)当方程有两个根,①若方程的两个根中只有一个正根,一个负根或零根,②若方程有两个正根,结合二次方程的根的情况可求.
解答:∵△=a
2-4(a
2-3)=12-3a
2(1)当方程只有一个根时,△=0,此时a=±2,
若a=2,此时方程x
2-2x+1=0的根x=1符合条件,
若a=-2,此时方程x
2+2x+1=0的根x=-1不符舍去,
(2)当方程有两个根时,△>0可得-2<a<2,
①若方程的两个根中只有一个正根,一个负根或零根,则有a
2-3≤0,解可得-

≤a≤

符合条件,
②若方程有两个正根,则

,
解可得
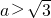
,
综上可得,-

≤a≤2.
故选D.
点评:本题考查了一元二次方程根的判别式的应用以及一元二次方程根的应用,是一个综合性的题目,也是一个难度中等的题目.

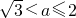

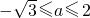
 ≤a≤
≤a≤ 符合条件,
符合条件, ,
,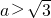 ,
, ≤a≤2.
≤a≤2.

 阅读快车系列答案
阅读快车系列答案