
将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
(1)如图①,对△ABC作变换[50°,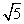 ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
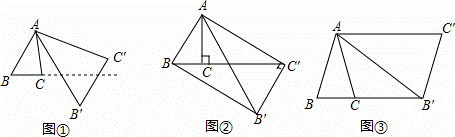
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上, 且四边形ABB'C'为矩形,求θ和n的值;
且四边形ABB'C'为矩形,求θ和n的值;
(4)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
(1). 5; 50° 
(2). θ=∠CAC'=∠BAC'﹣∠BAC=90°﹣30°=60°.
在 Rt△ABC 中,∠ABB'=90°,∠BAB'=60°∴∠AB'B=30°,
∴n=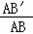 =2;
=2;
(3)∵四边形ABB'C'是平行四边形,∴AC'∥BB',又∵∠BAC=36°,
∴θ=∠CAC'=∠ACB=72°. 
∴∠C'AB'=∠BAC=36°,而∠B=∠B,∴△ABC∽△B'BA,
∴AB:BB'=CB:AB, ∴AB2=CB·BB'=CB(BC+CB'),
而 CB'=AC=AB=B'C', BC=1, ∴AB2=1(1+AB), ∴AB=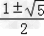 ,
,
∵AB>0, ∴n=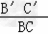 =
=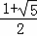 .
.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:初中数学 来源: 题型:
如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动 扶梯底端A处测得C点的仰角为42°,求二楼的层高BC约为多少米?( sin42°≈0.7,tan42°≈0.9)
扶梯底端A处测得C点的仰角为42°,求二楼的层高BC约为多少米?( sin42°≈0.7,tan42°≈0.9)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,将△ABC绕点A逆时针方向旋转到△ADE的位置,点B落在AC边上的点D处,
设旋转角为a (0°<a<90°).若ÐB=125°,ÐE=30°,则Ða= °.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com