
【题目】如图,在正方形![]() 中,点
中,点![]() 分别是
分别是![]() 上的两个动点(不与点
上的两个动点(不与点![]() 重合),且
重合),且![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() .
.
(1)依题意将图形补全;
(2)小华通过观察、实验、提出猜想:在点![]() 运动过程中,始终有
运动过程中,始终有![]() .经过与同学们充分讨论,形成了几种证明的想法:
.经过与同学们充分讨论,形成了几种证明的想法:
想法一:连接![]() ,证明
,证明![]() 是等腰直角三角形;
是等腰直角三角形;
想法二:过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 的延长线于
的延长线于![]() ,可得
,可得![]() 是等腰直角三角形,证明
是等腰直角三角形,证明![]() ;
;
……
请参考以上想法,帮助小华证明![]() .(写出一种方法即可)
.(写出一种方法即可)
【答案】(1)图见解析;(2)想法一的证明见解析;想法二的证明见解析.
【解析】
(1)先分别在![]() 上取点
上取点![]() ,使得
,使得![]() ,再延长
,再延长![]() 到
到![]() ,使
,使![]() ,然后连接
,然后连接![]() 即可;
即可;
(2)想法一:先根据正方形的性质、三角形全等的判定定理与性质得出![]() ,
,![]() ,再根据角的和差、等量代换可得
,再根据角的和差、等量代换可得![]() ,从而可得
,从而可得![]() 是等腰直角三角形,然后根据等腰直角三角形的性质可得
是等腰直角三角形,然后根据等腰直角三角形的性质可得![]() ,最后根据垂线平分线的判定与性质可得
,最后根据垂线平分线的判定与性质可得![]() ,由此即可得证;
,由此即可得证;
想法二:先根据正方形的性质、三角形全等的判定定理与性质得出![]() ,从而可得
,从而可得![]() 是等腰直角三角形,再根据等腰直角三角形的性质可得
是等腰直角三角形,再根据等腰直角三角形的性质可得![]() ,然后根据三角形全等的判定定理与性质得出
,然后根据三角形全等的判定定理与性质得出![]() ,由此即可得证.
,由此即可得证.
(1)先分别在![]() 上取点
上取点![]() ,使得
,使得![]() ,再延长
,再延长![]() 到
到![]() ,使
,使![]() ,然后连接
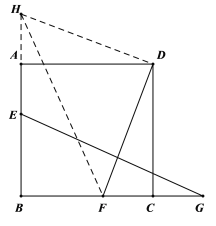
,然后连接![]() ,补全图形如下所示:
,补全图形如下所示:
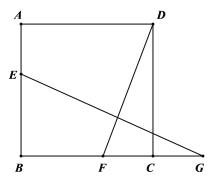
(2)想法一:如图,连接![]()
![]() 四边形ABCD是正方形
四边形ABCD是正方形
![]()
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,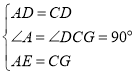
![]()
![]() ,
,![]()
![]()
![]() ,即
,即![]()
![]() 是等腰直角三角形
是等腰直角三角形
![]()
又![]()
![]() 是线段FG的垂直平分线
是线段FG的垂直平分线
![]()
![]() ;
;

想法二:如图,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 的延长线于
的延长线于![]() ,连接HF
,连接HF
![]() 四边形ABCD是正方形
四边形ABCD是正方形
![]()
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,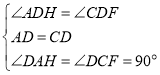
![]()
![]()
![]() 是等腰直角三角形
是等腰直角三角形
![]()
![]()
![]() ,即
,即![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,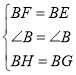
![]()
![]()
![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】五名学生投篮球,每人投10次,统计他们每人投中的次数.得到五个数据,并对数据进行整理和分析给出如下信息:
平均数 | 中位数 | 众数 |
m | 6 | 7 |
则下列选项正确的是( )
A.可能会有学生投中了8次
B.五个数据之和的最大值可能为30
C.五个数据之和的最小值可能为20
D.平均数m一定满足![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
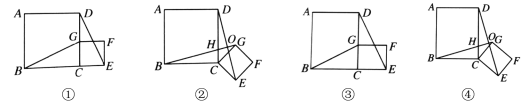
【题目】(1)在正方形ABCD中,G是CD边上的一个动点(不与C、D重合),以CG为边在正方形ABCD外作一个正方形CEFG,连结BG、DE,如图①.直接写出线段BG、DE的关系 ;
(2)将图①中的正方形CEFG绕点C按顺时针方向旋转任意角度![]() ,如图②,试判断(1)中的结论是否成立?若成立,直接写出结论,若不成立,说明理由;
,如图②,试判断(1)中的结论是否成立?若成立,直接写出结论,若不成立,说明理由;
(3)将(1)中的正方形都改为矩形,如图③,再将矩形CEFG绕点C按顺时针方向旋转任意角度![]() ,如图④,若AB=a,BC=b;CE =ka,CG=kb,(
,如图④,若AB=a,BC=b;CE =ka,CG=kb,(![]() )试判断(1)中的结论是否仍然成立?并说明理由.
)试判断(1)中的结论是否仍然成立?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
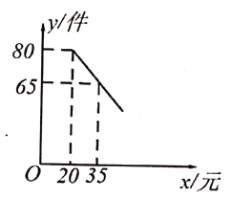
【题目】某超市购进一批成本为每件![]() 元的商品,经调查发现,该商品每天的销售量
元的商品,经调查发现,该商品每天的销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间满足一次函数关系,其图象如图所示.
(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量![]() 与销售单价
与销售单价![]() 之间的函数关系式;
之间的函数关系式;
(2)若超市按单价不低于成本价,且不高于![]() 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润
元销售,则销售单价定为多少,才能使销售该商品每天获得的利润![]() (元)最大?
(元)最大?
(3)若超市要使销售该商品每天获得的利润为![]() 元,则每天的销售量应为多少件?
元,则每天的销售量应为多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() ,
,![]() 两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
价格 类型 | 进价(元/盏) | 售价(元/盏) |
| 40 | 55 |
| 60 | 80 |
(1)若商场恰好用完预计进货款5500元,则应这购进两种台灯各多少盏?
(2)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本).
型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
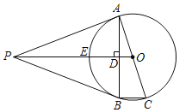
【题目】如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连接OP交⊙O于E.过A点作AB⊥PO于点D,交⊙O于B,连接BC,PB.
(1)求证:PB是⊙O的切线;
(2)求证:E为△PAB的内心;
(3)若cos∠PAB=![]() ,BC=1,求PO的长.
,BC=1,求PO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,隧道的截面由抛物线和长方形构成.长方形的长为16m,宽为6m,抛物线的最高点C离路面AA1的距离为8m.
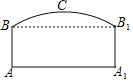
(1)建立适当的坐标系,求出表示抛物线的函数表达式;
(2)一大型货车装载设备后高为7m,宽为4m.如果隧道内设双向行驶车道,那么这辆货车能否安全通过?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com