【题目】若一个正多边形的每个外角都等于45°，则它是（ ）
A. 正六边形
B. 正八边形
C. 正十边形
D. 正十二边形
科目：初中数学 来源： 题型：
【题目】下列关于函数
的四个命题：①当
时，
有最小值10；②
为任意实数，
时的函数值大于
时的函数值；③若
，且
是整数，当
时，
的整数值有
个；④若函数图象过点
和
，其中
，
，则
．其中真命题的序号是（ ）
A．① B．② C．③ D．④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】综合题
（1）感知：如图①，四边形ABCD、CEFG均为正方形．易知BE=DG．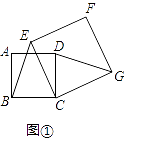
（2）探究：如图②，四边形ABCD、CEFG均为菱形，且∠A=∠F．求证：BE=DG．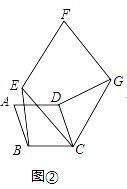
（3）如图③，四边形ABCD、CEFG均为菱形，点E在边AD上，点G在AD的延长线上．若AE=3ED，∠A=∠F，△EBC的面积为8，则菱形CEFG的面积为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】丽水某公司将“丽水山耕”农副产品运往杭州市场进行销售，记汽车行驶时为t小时，平均速度为v千米/小时（汽车行驶速度不超过100千米/小时）．根据经验，v，t的一组对应值如下表：
（1）根据表中的数据，求出平均速度v（千米/小时）关于行驶时间t（小时）的函数表达式；
（2）汽车上午7：30从丽水出发，能否在上午00之前到达杭州市场？请说明理由；
（3）若汽车到达杭州市场的行驶时间t满足3.5≤t≤4，求平均速度v的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，在△ABC中，∠A=30°，点P从点A出发以2cm/s的速度沿折线A﹣C﹣B运动，点Q从点A出发以a（cm/s）的速度沿AB运动，P，Q两点同时出发，当某一点运动到点B时，两点同时停止运动．设运动时间为x（s），△APQ的面积为y（cm2），y关于x的函数图象由C1，C2两段组成，如图2所示．
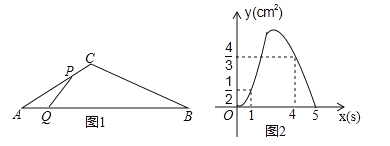
（1）求a的值；
（2）求图2中图象C2段的函数表达式；
（3）当点P运动到线段BC上某一段时△APQ的面积，大于当点P在线段AC上任意一点时△APQ的面积，求x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】国家发改委已于2012年5月24日核准广东湛江钢铁基地项目，项目由宝钢湛江钢铁有限公司投资建设，预计投产后年产10200000吨钢铁，数据10200000用科学记数法表示为（ ）
A.102×105
B.10.2×106
C.1.02×106
D.1.02×107
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2017年5月14日至15日，“一带一路”国际合作高峰论坛在北京举行，本届论坛期间，中国同30多个国家签署经贸合作协议，某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区，已知2件甲种商品与3件乙种商品的销售收入相同，3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元？
(2)若甲、乙两种商品的销售总收入不低于5400万元，则至少销售甲种商品多少万件？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平面直角坐标系中，直线l：y=﹣ 
x+ 分别交x轴，y轴于A，B两点，点C在x轴负半轴上，且∠ACB=30°．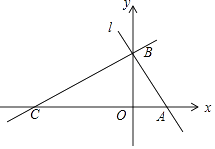
（1）求A，C两点的坐标．
（2）若点M从点C出发，以每秒1个单位长度的速度沿射线CB运动，连接AM，设△ABM的面积为S，点M的运动时间为t，求出S关于t的函数关系式，并写出自变量的取值范围．
（3）点P是y轴上的点，在坐标平面内是否存在点Q，使以A，B，P，Q为顶点的四边形是菱形？若存在，请直接写出Q点的坐标；若不存在，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
