
����Ŀ����ͼ1������ABC�У���A=30�㣬��P�ӵ�A������2cm/s���ٶ�������A��C��B�˶�����Q�ӵ�A������a��cm/s�����ٶ���AB�˶���P��Q����ͬʱ��������ijһ���˶�����Bʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊx��s������APQ�����Ϊy��cm2����y����x�ĺ���ͼ����C1��C2������ɣ���ͼ2��ʾ��
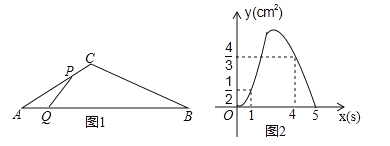
��1����a��ֵ��
��2����ͼ2��ͼ��C2�εĺ�������ʽ��
��3������P�˶����߶�BC��ijһ��ʱ��APQ����������ڵ���P���߶�AC������һ��ʱ��APQ���������x��ȡֵ��Χ��
���𰸡���1��1����2��![]() ����3��2��x��3��
����3��2��x��3��
��������
�����������1����PD��AB��D������ֱ�������ε����ʵõ�PD=![]() AP=x�����������ε������ʽ�õ���������ʽ��������㣻
AP=x�����������ε������ʽ�õ���������ʽ��������㣻
��2�����ݵ�x=4ʱ��y=![]() �����sinB���õ�ͼ��C2�εĺ�������ʽ��
�����sinB���õ�ͼ��C2�εĺ�������ʽ��
��3�����![]() �����ֵ�����ݶ��κ��������ʼ��㼴�ɣ�
�����ֵ�����ݶ��κ��������ʼ��㼴�ɣ�
�����������1����ͼ1����PD��AB��D���ߡ�A=30�㣬��PD=![]() AP=x����y=
AP=x����y=![]() AQPD=
AQPD=![]() ����ͼ���֪����x=1ʱ��y=
����ͼ���֪����x=1ʱ��y=![]() ����
����![]() ��a��12=
��a��12=![]() ����ã�a=1��
����ã�a=1��
��2����ͼ2����PD��AB��D����ͼ���֪��PB=5��2��2x=10��2x��PD=PBsinB=��10��2x��sinB����y=![]() ��AQ��PD=
��AQ��PD=![]() x����10��2x��sinB������x=4ʱ��y=
x����10��2x��sinB������x=4ʱ��y=![]() ����
����![]() ��4����10��2��4��sinB=
��4����10��2��4��sinB=![]() ����ã�sinB=
����ã�sinB=![]() ����y=
����y=![]() x����10��2x����
x����10��2x����![]() ����
����![]() ��
��
��3��![]() ����ã�x1=0��x2=2����ͼ���֪����x=2ʱ��
����ã�x1=0��x2=2����ͼ���֪����x=2ʱ��![]() �����ֵ�����ֵ��
�����ֵ�����ֵ��![]() ��22=2��
��22=2��![]() =2����ã�x1=3��x2=2������2��x��3ʱ����P�˶����߶�BC��ijһ��ʱ��APQ����������ڵ���P���߶�AC������һ��ʱ��APQ�������
=2����ã�x1=3��x2=2������2��x��3ʱ����P�˶����߶�BC��ijһ��ʱ��APQ����������ڵ���P���߶�AC������һ��ʱ��APQ�������




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������б��еĶ�Ӧֵ��
x | 2.1 | 2.2 | 2.3 | 2.4 |
ax2+bx+c | ��1.39 | ��0.76 | ��0.11 | 0.56 |
�жϷ���ax2+bx+c=0��a��0��a��b��cΪ��������һ�����ȡֵ��ΧΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У��ı���![]() �����������ֱ�Ϊ
�����������ֱ�Ϊ![]() ������
������![]() ��
��![]() ͬʱ��
ͬʱ��![]() ��������˶�ʱ��Ϊ
��������˶�ʱ��Ϊ![]() �룬��
�룬��![]() ��
��![]() ������
������![]() ��λ����/����ٶ����
��λ����/����ٶ����![]() �˶�����
�˶�����![]() ������
������![]() �˶�����
�˶�����![]() ���˶����ٶȷֱ�Ϊ
���˶����ٶȷֱ�Ϊ![]() ����λ����/�룩.��
����λ����/�룩.��![]() �е�һ�㵽��
�е�һ�㵽��![]() ��ʱ������ͬʱֹͣ�˶�.
��ʱ������ͬʱֹͣ�˶�.
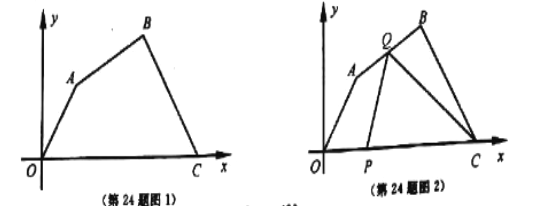
��1����![]() ����ֱ�ߵĺ�������ʽ��
����ֱ�ߵĺ�������ʽ��
��2����ͼ2������![]() ��
��![]() ���˶�ʱ����
���˶�ʱ����![]() �����
�����![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��![]() �����ֵ��
�����ֵ��
��3����![]() ��
��![]() ���˶������У����߶�
���˶������У����߶�![]() �Ĵ�ֱƽ���߾����ı���
�Ĵ�ֱƽ���߾����ı���![]() �Ķ��㣬����Ӧ��
�Ķ��㣬����Ӧ��![]() ֵ.
ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=Rt������BCΪֱ������O��AB�ڵ�D������DE��AC�ڵ�E��
��1����֤����A=��ADE��
��2����AD=16��DE=10����BC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��������ε�ÿ����Ƕ�����45�㣬�������� ��
A. ��������
B. ���˱���
C. ��ʮ����
D. ��ʮ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��Ķ����ɭ�ֹ�ռ��3 980 000ƽ���ף�λ�ڱ������������ߵı������ϣ�����������ʮ����ˮ��ͨ�������л�����ϵ��һ����������ʵ�ı����ġ�������������3 980 000�ÿ�ѧ��������ʾΪ�� ��
A.39.8��105
B.3.98��106
C.3.98��107
D.0.398��107
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽ⱾУ���꼶ͬѧ��˫���ղμ�����������ʱ�䣬����С��������ʾ����飨�ʾ��������ͼ��ʾ�������õ�����������ͼ1��ͼ2����ͳ��ͼ�������������������ͳ��ͼ����������⣺
 ��1�����ν����ʾ������ͬѧ�ж����ˣ���ȫ����ͳ��ͼ��
��1�����ν����ʾ������ͬѧ�ж����ˣ���ȫ����ͳ��ͼ��
��2����У�����꼶ͬѧ800�ˣ�����˫���ղμ���������ʱ����3Сʱ���ڣ�����3Сʱ����������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com