
【题目】如图,平面直角坐标系中,直线l:y=﹣ ![]() x+
x+ ![]() 分别交x轴,y轴于A,B两点,点C在x轴负半轴上,且∠ACB=30°.
分别交x轴,y轴于A,B两点,点C在x轴负半轴上,且∠ACB=30°.
(1)求A,C两点的坐标.
(2)若点M从点C出发,以每秒1个单位长度的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,求出S关于t的函数关系式,并写出自变量的取值范围.
(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A,B,P,Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,说明理由.
【答案】
(1)解:当x=0时,y= ![]() ;当y=0时,x=1.
;当y=0时,x=1.
∴点A坐标为(1,0),点B坐标为(0, ![]() ),
),
在Rt△BOC中,∠OCB=30°,OB= ![]() ,
,
∴BC=2 ![]() .
.
∴OC= ![]() =3.
=3.
∴点C坐标为(﹣3,0).
(2)解:如图1所示:
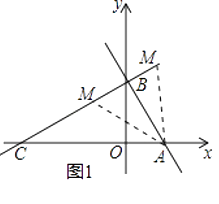
∵OA=1,OB= ![]() ,AB=2,
,AB=2,
∴∠ABO=30°,
同理:BC=2 ![]() ,∠OCB=30°,
,∠OCB=30°,
∴∠OBC=60°,
∴∠ABC=90°,
分两种情况考虑:若M在线段BC上时,BC=2 ![]() ,CM=t,可得BM=BC﹣CM=2
,CM=t,可得BM=BC﹣CM=2 ![]() ﹣t,
﹣t,
此时S△ABM= ![]() BMAB=
BMAB= ![]() ×(2
×(2 ![]() ﹣t)×2=2
﹣t)×2=2 ![]() ﹣t(0≤t<2
﹣t(0≤t<2 ![]() );
);
若M在BC延长线上时,BC=2 ![]() ,CM=t,可得BM=CM﹣BC=t﹣2
,CM=t,可得BM=CM﹣BC=t﹣2 ![]() ,
,
此时S△ABM= ![]() BMAB=
BMAB= ![]() ×(t﹣2
×(t﹣2 ![]() )×2=t﹣2
)×2=t﹣2 ![]() (t≥2
(t≥2 ![]() );
);
综上所述,S= ![]() ;
;
(3)解:P是y轴上的点,在坐标平面内存在点Q,使以 A、B、P、Q为顶点的四边形是菱形,
如2图所示,
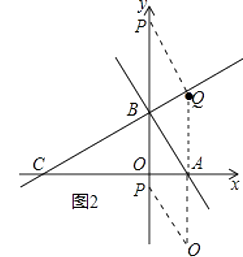
当P在y轴正半轴上,四边形ABPQ为菱形,①可得AQ=AB=2,且Q与A的横坐标相同,
此时Q坐标为(1,2),②AP=AQ= ![]() ,Q与A的横坐标相同,此时Q坐标为(1,
,Q与A的横坐标相同,此时Q坐标为(1, ![]() ),
),
当P在y轴负半轴上,四边形ABPQ为菱形,①可得AQ=AB=2,且Q与A横坐标相同,
此时Q坐标为(1,﹣2),②BP垂直平分AQ,此时Q坐标为(﹣1,0),
综上,满足题意Q坐标为(1,2)、(1,﹣2)、(1, ![]() )、(﹣1,0).
)、(﹣1,0).
【解析】(1)直线y=-![]() x+
x+![]() 分别交x轴,y轴于A,B两点,点C在x轴负半轴上,当x=0时,y=
分别交x轴,y轴于A,B两点,点C在x轴负半轴上,当x=0时,y=![]() ;当y=0时,x=1;所以点A坐标为(1,0),点B坐标为(0,
;当y=0时,x=1;所以点A坐标为(1,0),点B坐标为(0, ![]() ),在Rt△BOC中,∠OCB=30°,OB=
),在Rt△BOC中,∠OCB=30°,OB=![]() ,得到BC=2
,得到BC=2![]() ,得到 OC=3,即点C坐标为(﹣3,0);(2)OA=1,OB=
,得到 OC=3,即点C坐标为(﹣3,0);(2)OA=1,OB=![]() ,AB=2,得到∠ABO=30°,同理:BC=2
,AB=2,得到∠ABO=30°,同理:BC=2![]() ,∠OCB=30°,得到∠OBC=60°,∠ABC=90°,分两种情况考虑:若M在线段BC上时,BC=2
,∠OCB=30°,得到∠OBC=60°,∠ABC=90°,分两种情况考虑:若M在线段BC上时,BC=2![]() ,CM=t,可得BM=BC﹣CM=2
,CM=t,可得BM=BC﹣CM=2![]() ﹣t,此时S△ABM=BMAB÷2=(2
﹣t,此时S△ABM=BMAB÷2=(2![]() ﹣t)×2÷2=2
﹣t)×2÷2=2![]() ﹣t(0≤t<2
﹣t(0≤t<2![]() );若M在BC延长线上时,BC=2
);若M在BC延长线上时,BC=2![]() ,CM=t,可得BM=CM﹣BC=t﹣2
,CM=t,可得BM=CM﹣BC=t﹣2 ![]() ,此时S△ABM=BMAB÷2=(t﹣2
,此时S△ABM=BMAB÷2=(t﹣2![]() )×2÷2=t﹣2
)×2÷2=t﹣2![]() (t≥2
(t≥2![]() );(3)当P在y轴正半轴上,四边形ABPQ为菱形,①可得AQ=AB=2,且Q与A的横坐标相同,此时Q坐标为(1,2),②AP=AQ= 2
);(3)当P在y轴正半轴上,四边形ABPQ为菱形,①可得AQ=AB=2,且Q与A的横坐标相同,此时Q坐标为(1,2),②AP=AQ= 2![]() ÷3 ,Q与A的横坐标相同,此时Q坐标为(1, 2
÷3 ,Q与A的横坐标相同,此时Q坐标为(1, 2![]() ÷3),当P在y轴负半轴上,四边形ABPQ为菱形,①可得AQ=AB=2,且Q与A横坐标相同,此时Q坐标为(1,﹣2),②BP垂直平分AQ,此时Q坐标为(﹣1,0),综上,满足题意Q坐标为(1,2)、(1,﹣2)、(1, 2
÷3),当P在y轴负半轴上,四边形ABPQ为菱形,①可得AQ=AB=2,且Q与A横坐标相同,此时Q坐标为(1,﹣2),②BP垂直平分AQ,此时Q坐标为(﹣1,0),综上,满足题意Q坐标为(1,2)、(1,﹣2)、(1, 2![]() ÷3 )、(﹣1,0).
÷3 )、(﹣1,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某文具厂计划加工3000套画图工具,为了尽快完成任务,实际每天加工画图工具的数量是原计划的1.2倍,结果提前4天完成任务,求该文具厂原计划每天加工这种画图工具的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大黄鱼是中国特有的地方性鱼类,有“国鱼”之称,由于过去滥捕等多种因素,大黄鱼资源已基本枯竭,目前,我市已培育出十余种大黄鱼品种,某鱼苗人工养殖基地对其中的四个品种“宁港”、“御龙”、“甬岱”、“象山港”共300尾鱼苗进行成活实验,从中选出成活率最高的品种进行推广,通过实验得知“甬岱”品种鱼苗成活率为![]() ,并把实验数据绘制成下列两幅统计图(部分信息未给出):
,并把实验数据绘制成下列两幅统计图(部分信息未给出):
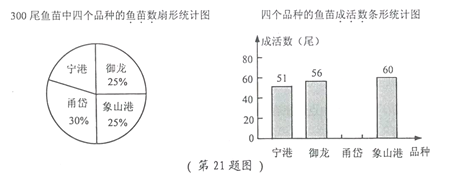
(1) 求实验中“宁港”品种鱼苗的数量;
(2) 求实验中“甬岱”品种鱼苗的成活数,并补全条形统计图;
(3)你认为应选哪一品种进行推广?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】昌平万亩滨河森林公园占地3 980 000平方米,位于北京城市中轴线的北延线上,将北京城与十三陵水库通过绿轴有机地联系在一起,是名副其实的北京的“后花园”.把数字3 980 000用科学记数法表示为( )
A.39.8×105
B.3.98×106
C.3.98×107
D.0.398×107
查看答案和解析>>
科目:初中数学 来源: 题型:
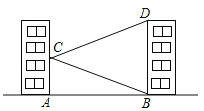
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(1)求∠BCD的度数.
(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com