练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知△ABC，AB=AC，将△ABC沿边BC翻折，得到的△DBC与原△ABC拼成四边形ABDC．求证：四边形ABDC是菱形．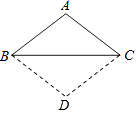

    【答案】解：由翻转变换的性质可知，BA=BD，CA=CD，

    ∵AB=AC，

    ∴AB=BD=DC=CA，

    ∴四边形ABDC是菱形


    【解析】由翻转变换的性质可知，BA=BD，CA=CD，由AB=AC，得到AB=BD=DC=CA，所以四边形ABDC是菱形.
    【考点精析】本题主要考查了等腰三角形的性质和菱形的判定方法的相关知识点，需要掌握等腰三角形的两个底角相等（简称：等边对等角）；任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】综合题
    （1）感知：如图①，四边形ABCD、CEFG均为正方形．易知BE=DG．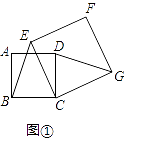

    （2）探究：如图②，四边形ABCD、CEFG均为菱形，且∠A=∠F．求证：BE=DG．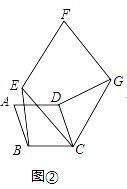

    （3）如图③，四边形ABCD、CEFG均为菱形，点E在边AD上，点G在AD的延长线上．若AE=3ED，∠A=∠F，△EBC的面积为8，则菱形CEFG的面积为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2017年5月14日至15日，“一带一路”国际合作高峰论坛在北京举行，本届论坛期间，中国同30多个国家签署经贸合作协议，某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区，已知2件甲种商品与3件乙种商品的销售收入相同，3件甲种商品比2件乙种商品的销售收入多1500元.

    (1)甲种商品与乙种商品的销售单价各多少元？

    (2)若甲、乙两种商品的销售总收入不低于5400万元，则至少销售甲种商品多少万件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平面直角坐标系中，直线l：y=﹣ x+ 分别交x轴，y轴于A，B两点，点C在x轴负半轴上，且∠ACB=30°．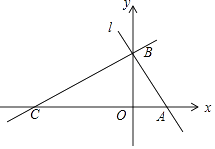

    （1）求A，C两点的坐标．
    （2）若点M从点C出发，以每秒1个单位长度的速度沿射线CB运动，连接AM，设△ABM的面积为S，点M的运动时间为t，求出S关于t的函数关系式，并写出自变量的取值范围．
    （3）点P是y轴上的点，在坐标平面内是否存在点Q，使以A，B，P，Q为顶点的四边形是菱形？若存在，请直接写出Q点的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为鼓励节约用水，某市自来水公司对居民用水采用以户为单位分段计费办法收费，即一个月用水10t以内（包含10t）的用户，收水费a元/t，一月用水超过10t的用户，超出的部分按b元/t（b＞a）收费，设一户居民用水x t，应收水费y元，y与x之间的函数关系式如图所示：按上述分段收费标准，小兰家3月份和4月份分别交水费29.1元和20.8元，则小兰家4月份比3月份节约用水吨．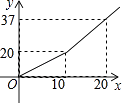

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】根据题意，解答下列问题：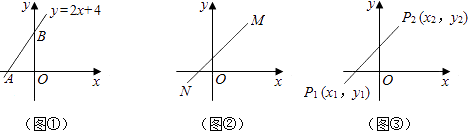

    （1）如图①，已知直线y=2x+4与x轴、y轴分别交于A、B两点，求线段AB的长；
    （2）如图②，类比（1）的求解过程，请你通过构造直角三角形的方法，求出两点M（3，4），N（﹣2，﹣1）之间的距离；
    （3）如图③，P1（x1 ， y1），P2（x2 ， y2）是平面直角坐标系内的两点，请你利用图③构造直角三角形，并直接写出P1P2的长度（用含有x1 ， x2 ， y1 ， y2的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图为某城市部分街道示意图，四边形ABCD为正方形，点G在对角线BD上，GE⊥CD，GF⊥BC，AD=1500m，小敏行走的路线为B→A→G→E，小聪行走的路线为B→A→D→E→F．若小敏行走的路程为3100m，则小聪行走的路程为 m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：（3x﹣1）（x﹣2）=______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列式子正确的（　　）

    A. x﹣（y﹣z）＝x﹣y﹣zB. ﹣a+b+c+d＝﹣（a﹣b）﹣（﹣c﹣d）

    C. x+2y﹣2z＝x﹣2（z+y）D. ﹣（x﹣y+z）＝﹣x﹣y﹣z

    查看答案和解析>>

    同步练习册答案