
ЁОЬтФПЁПИљОнЬтвтЃЌНтД№ЯТСаЮЪЬтЃК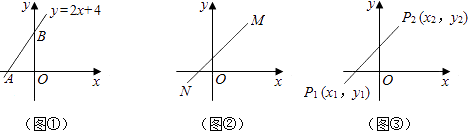
ЃЈ1ЃЉШчЭМЂйЃЌвбжЊжБЯпy=2x+4гыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌЧѓЯпЖЮABЕФГЄЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌРрБШЃЈ1ЃЉЕФЧѓНтЙ§ГЬЃЌЧыФуЭЈЙ§ЙЙдьжБНЧШ§НЧаЮЕФЗНЗЈЃЌЧѓГіСНЕуMЃЈ3ЃЌ4ЃЉЃЌNЃЈЉ2ЃЌЉ1ЃЉжЎМфЕФОрРыЃЛ
ЃЈ3ЃЉШчЭМЂлЃЌP1ЃЈx1 ЃЌ y1ЃЉЃЌP2ЃЈx2 ЃЌ y2ЃЉЪЧЦНУцжБНЧзјБъЯЕФкЕФСНЕуЃЌЧыФуРћгУЭМЂлЙЙдьжБНЧШ§НЧаЮЃЌВЂжБНгаДГіP1P2ЕФГЄЖШЃЈгУКЌгаx1 ЃЌ x2 ЃЌ y1 ЃЌ y2ЕФДњЪ§ЪНБэЪОЃЉЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКШчЭМЂйЃЌгЩy=0ЕУЃЌ2x+4=0ЃЌ
x=Љ2ЃЌ
ЁрAЃЈЉ2ЃЌ0ЃЉЃЌ
ЁрOA=2ЃЌ
ЕБx=0ЪБЃЌy=4ЃЌ
ЁрBЃЈ0ЃЌ4ЃЉЃЌ
ЁрOB=4ЃЌ
дкRtЁїAOBжаЃЌгЩЙДЙЩЖЈРэЕУЃКAB= ![]() =2
=2 ![]()
ЃЈ2ЃЉНтЃКШчЭМЂкЃЌЙ§MзїMPЁЭxжсЃЌЙ§NзїNPЁЭyжсЃЌMPКЭNPНЛгкPЃЌдђMPЁЭNPЃЌ
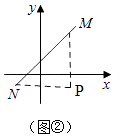
ЁпMЃЈ3ЃЌ4ЃЉЃЌNЃЈЉ2ЃЌЉ1ЃЉЃЌ
ЁрPЃЈ3ЃЌЉ1ЃЉЃЌ
ЁрMP=4ЉЃЈЉ1ЃЉ=5ЃЌNP=3ЉЃЈЉ2ЃЉ=5ЃЌ
дкRtЁїMNPжаЃЌгЩЙДЙЩЖЈРэЕУЃКMN= ![]() =5
=5 ![]()
ЃЈ3ЃЉНтЃКШчЭМЂлЃЌЙ§P2зїP2PЁЭxжсЃЌЙ§P1зїP1PЁЭyжсЃЌP1PКЭP2PНЛгкPЃЌдђP1PЁЭP2PЃЌ
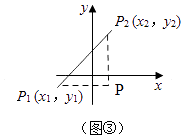
ЁпP1ЃЈx1ЃЌy1ЃЉЃЌP2ЃЈx2ЃЌy2ЃЉЃЌ
ЁрPЃЈx1ЃЌy1ЃЉЃЌ
ЁрP1P=x2Љx1ЃЌP2P=y2Љy1ЃЌ
дкRtЁїP1P2PжаЃЌгЩЙДЙЩЖЈРэЕУЃКP1P2= ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЃЈ1ЃЉШчЭМЂйЃЌгЩy=0ЕУЃЌ2x+4=0ЃЌЕУЕНx=Љ2ЃЌAЃЈЉ2ЃЌ0ЃЉЃЌЕУЕНOA=2ЃЌЕБx=0ЪБЃЌy=4ЃЌЕУЕНBЃЈ0ЃЌ4ЃЉЃЌOB=4ЃЌдкRtЁїAOBжаЃЌгЩЙДЙЩЖЈРэЕУЃКAB=![]() =2
=2![]() ЃЛЃЈ2ЃЉШчЭМЂкЃЌЙ§MзїMPЁЭxжсЃЌЙ§NзїNPЁЭyжсЃЌMPКЭNPНЛгкPЃЌдђMPЁЭNPЃЌЕУЕНMЃЈ3ЃЌ4ЃЉЃЌNЃЈЉ2ЃЌЉ1ЃЉЃЌPЃЈ3ЃЌЉ1ЃЉЫљвдMP=4ЉЃЈЉ1ЃЉ=5ЃЌNP=3ЉЃЈЉ2ЃЉ=5ЃЌдкRtЁїMNPжаЃЌгЩЙДЙЩЖЈРэЕУЃКMN=
ЃЛЃЈ2ЃЉШчЭМЂкЃЌЙ§MзїMPЁЭxжсЃЌЙ§NзїNPЁЭyжсЃЌMPКЭNPНЛгкPЃЌдђMPЁЭNPЃЌЕУЕНMЃЈ3ЃЌ4ЃЉЃЌNЃЈЉ2ЃЌЉ1ЃЉЃЌPЃЈ3ЃЌЉ1ЃЉЫљвдMP=4ЉЃЈЉ1ЃЉ=5ЃЌNP=3ЉЃЈЉ2ЃЉ=5ЃЌдкRtЁїMNPжаЃЌгЩЙДЙЩЖЈРэЕУЃКMN=![]() =5
=5![]() ЃЛЃЈ3ЃЉШчЭМЂлЃЌЙ§P2зїP2PЁЭxжсЃЌЙ§P1зїP1PЁЭyжсЃЌP1PКЭP2PНЛгкPЃЌдђP1PЁЭP2PЃЌвђЮЊP1ЃЈx1ЃЌy1ЃЉЃЌP2ЃЈx2ЃЌy2ЃЉЃЌЕУЕНPЃЈx1ЃЌy1ЃЉЃЌЫљвдP1P=x2Љx1ЃЌP2P=y2Љy1ЃЌдкRtЁїP1P2PжаЃЌгЩЙДЙЩЖЈРэЕУЃКP1P22=ЃЈx2-x1 ЃЉ2+ЃЈy2-y1ЃЉ2.
ЃЛЃЈ3ЃЉШчЭМЂлЃЌЙ§P2зїP2PЁЭxжсЃЌЙ§P1зїP1PЁЭyжсЃЌP1PКЭP2PНЛгкPЃЌдђP1PЁЭP2PЃЌвђЮЊP1ЃЈx1ЃЌy1ЃЉЃЌP2ЃЈx2ЃЌy2ЃЉЃЌЕУЕНPЃЈx1ЃЌy1ЃЉЃЌЫљвдP1P=x2Љx1ЃЌP2P=y2Љy1ЃЌдкRtЁїP1P2PжаЃЌгЩЙДЙЩЖЈРэЕУЃКP1P22=ЃЈx2-x1 ЃЉ2+ЃЈy2-y1ЃЉ2.
ЁОПМЕуОЋЮіЁПНтД№ДЫЬтЕФЙиМќдкгкРэНтвЛДЮКЏЪ§ЕФаджЪЕФЯрЙижЊЪЖЃЌеЦЮевЛАуЕиЃЌвЛДЮКЏЪ§y=kx+bгаЯТСааджЪЃКЃЈ1ЃЉЕБk>0ЪБЃЌyЫцxЕФдіДѓЖјдіДѓЃЈ2ЃЉЕБk<0ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁЃЎ


 жаПМНтЖСПМЕуОЋСЗЯЕСаД№АИ
жаПМНтЖСПМЕуОЋСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЭЌвЛЬѕЕРТЗЩЯЃЌМзГЕДгAЕиЕНBЕиЃЌввГЕДгBЕиЕНAЕиЃЌввЯШГіЗЂЃЌЭМжаЕФелЯпЖЮБэЪОМзЁЂввСНГЕжЎМфЕФОрРыyЃЈЧЇУзЃЉгыааЪЛЪБМфxЃЈаЁЪБЃЉЕФКЏЪ§ЙиЯЕЕФЭМЯѓЃЌЯТСаЫЕЗЈДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ
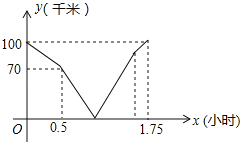
A. ввЯШГіЗЂЕФЪБМфЮЊ0.5аЁЪБ B. МзЕФЫйЖШЪЧ80ЧЇУз/аЁЪБ
C. МзГіЗЂ0.5аЁЪБКѓСНГЕЯргі D. МзЕНBЕиБШввЕНAЕидч![]() аЁЪБ
аЁЪБ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДѓЛЦгуЪЧжаЙњЬигаЕФЕиЗНадгуРрЃЌгаЁАЙњгуЁБжЎГЦЃЌгЩгкЙ§ШЅРФВЖЕШЖржжвђЫиЃЌДѓЛЦгузЪдДвбЛљБОПнНпЃЌФПЧАЃЌЮвЪавбХрг§ГіЪЎгржжДѓЛЦгуЦЗжжЃЌФГгуУчШЫЙЄбјжГЛљЕиЖдЦфжаЕФЫФИіЦЗжжЁАФўИлЁБЁЂЁАгљСњЁБЁЂЁА№ЎсЗЁБЁЂЁАЯѓЩНИлЁБЙВ300ЮВгуУчНјааГЩЛюЪЕбщЃЌДгжабЁГіГЩЛюТЪзюИпЕФЦЗжжНјааЭЦЙуЃЌЭЈЙ§ЪЕбщЕУжЊЁА№ЎсЗЁБЦЗжжгуУчГЩЛюТЪЮЊ![]() ЃЌВЂАбЪЕбщЪ§ОнЛцжЦГЩЯТСаСНЗљЭГМЦЭМ(ВПЗжаХЯЂЮДИјГі)ЃК
ЃЌВЂАбЪЕбщЪ§ОнЛцжЦГЩЯТСаСНЗљЭГМЦЭМ(ВПЗжаХЯЂЮДИјГі)ЃК
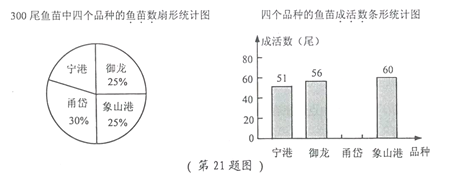
(1) ЧѓЪЕбщжаЁАФўИлЁБЦЗжжгуУчЕФЪ§СПЃЛ
(2) ЧѓЪЕбщжаЁА№ЎсЗЁБЦЗжжгуУчЕФГЩЛюЪ§ЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЛ
(3)ФуШЯЮЊгІбЁФФвЛЦЗжжНјааЭЦЙуЃПЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCЃЌAB=ACЃЌНЋЁїABCбиБпBCЗелЃЌЕУЕНЕФЁїDBCгыдЁїABCЦДГЩЫФБпаЮABDCЃЎЧѓжЄЃКЫФБпаЮABDCЪЧСтаЮЃЎ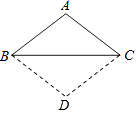
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКШчЭМ1ЃЌХзЮяЯп![]() гы
гы![]() жсНЛгкAЃЌBСНЕуЃЌЕуPдкХзЮяЯпЩЯЃЈЕуPгыAЃЌBСНЕуВЛжиКЯЃЉЃЌШчЙћЁїABPЕФШ§БпТњзу
жсНЛгкAЃЌBСНЕуЃЌЕуPдкХзЮяЯпЩЯЃЈЕуPгыAЃЌBСНЕуВЛжиКЯЃЉЃЌШчЙћЁїABPЕФШ§БпТњзу![]() ЃЌдђГЦЕуPЮЊХзЮяЯп
ЃЌдђГЦЕуPЮЊХзЮяЯп![]() ЕФЙДЙЩЕуЁЃ
ЕФЙДЙЩЕуЁЃ
ЃЈ1ЃЉжБНгаДГіХзЮяЯп![]() ЕФЙДЙЩЕуЕФзјБъЃЛ
ЕФЙДЙЩЕуЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌвбжЊХзЮяЯпCЃК![]() гы
гы![]() жсНЛгкAЃЌBСНЕуЃЌЕуPЃЈ1ЃЌ
жсНЛгкAЃЌBСНЕуЃЌЕуPЃЈ1ЃЌ![]() ЃЉЪЧХзЮяЯпCЕФЙДЙЩЕуЃЌЧѓХзЮяЯпCЕФКЏЪ§БэДяЪНЃЛ
ЃЉЪЧХзЮяЯпCЕФЙДЙЩЕуЃЌЧѓХзЮяЯпCЕФКЏЪ§БэДяЪНЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕуQдкХзЮяЯпCЩЯЃЌЧѓТњзуЬѕМў![]() ЕФЕуQЃЈвьгкЕуPЃЉЕФзјБъ
ЕФЕуQЃЈвьгкЕуPЃЉЕФзјБъ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
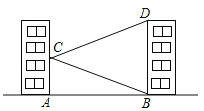
ЁОЬтФПЁПШчЭМЃЌбЇаЃЕФЪЕбщТЅЖдУцЪЧвЛДБНЬбЇТЅЃЌаЁУєдкЪЕбщТЅЕФДАПкCВтЕУНЬбЇТЅЖЅВПDЕФбіНЧЮЊ18ЁуЃЌНЬбЇТЅЕзВПBЕФИЉНЧЮЊ20ЁуЃЌСПЕУЪЕбщТЅгыНЬбЇТЅжЎМфЕФОрРыAB=30mЃЎ
ЃЈ1ЃЉЧѓЁЯBCDЕФЖШЪ§ЃЎ
ЃЈ2ЃЉЧѓНЬбЇТЅЕФИпBDЃЎЃЈНсЙћОЋШЗЕН0.1mЃЌВЮПМЪ§ОнЃКtan20ЁуЁж0.36ЃЌtan18ЁуЁж0.32ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЗНГЬжаЪЧЖўдЊвЛДЮЗНГЬЕФЪЧЃЈ ЃЉ
A.3x+y=0
B.2xЉ1=4
C.2x2Љy=2
D.2x+y=3z
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com