
【题目】定义:如图1,抛物线![]() 与
与![]() 轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足
轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足![]() ,则称点P为抛物线
,则称点P为抛物线![]() 的勾股点。
的勾股点。
(1)直接写出抛物线![]() 的勾股点的坐标;
的勾股点的坐标;
(2)如图2,已知抛物线C:![]() 与
与![]() 轴交于A,B两点,点P(1,
轴交于A,B两点,点P(1,![]() )是抛物线C的勾股点,求抛物线C的函数表达式;
)是抛物线C的勾股点,求抛物线C的函数表达式;
(3)在(2)的条件下,点Q在抛物线C上,求满足条件![]() 的点Q(异于点P)的坐标
的点Q(异于点P)的坐标

【答案】(1)(0,1);(2)y=﹣![]() x2+
x2+![]() x;(3)(3,
x;(3)(3,![]() )或(2+
)或(2+![]() ,﹣
,﹣![]() )或(2﹣
)或(2﹣![]() ,﹣
,﹣![]() ).
).
【解析】
试题分析:(1)根据抛物线勾股点的定义即可求解;
(2)作PG⊥x轴,由P点坐标求得AG=1、PG=![]() 、 PA=2,由tan∠PAB=
、 PA=2,由tan∠PAB=![]() 知∠PAG=60°,从而求得AB=4,即B(4,0),运用待定系数法即可求解;
知∠PAG=60°,从而求得AB=4,即B(4,0),运用待定系数法即可求解;
(3)由SΔABQ=SΔABP且两三角形同底,可知点Q到x轴的距离为![]() ,据此可求解.
,据此可求解.
试题解析: (1)抛物线y=﹣x2+1的勾股点的坐标为(0,1);
(2)抛物线y=ax2+bx过原点,即点A(0,0),
如图,作PG⊥x轴于点G,
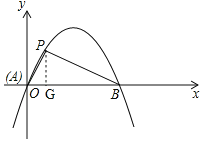
∵点P的坐标为(1,![]() ),
),
∴AG=1、PG=![]() ,PA=
,PA=![]() =2,
=2,
∵tan∠PAB=![]() ,
,
∴∠PAG=60°,
在Rt△PAB中,AB=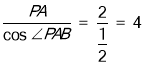 ,
,
∴点B坐标为(4,0),
设y=ax(x﹣4),
将点P(1,![]() )代入得:a=﹣
)代入得:a=﹣![]() ,
,
∴y=﹣![]() x(x﹣4)=﹣
x(x﹣4)=﹣![]() x2+
x2+![]() x;
x;
(3)①当点Q在x轴上方时,由S△ABQ=S△ABP知点Q的纵坐标为![]() ,
,
则有﹣![]() x2+
x2+![]() x =
x =![]() ,
,
解得:x1=3,x2=1(不符合题意,舍去),
∴点Q的坐标为(3,![]() );
);
②当点Q在x轴下方时,由S△ABQ=S△ABP知点Q的纵坐标为﹣![]()
则有﹣![]() x2+
x2+![]() x =﹣
x =﹣![]() ,
,
解得:x1=2+![]() ,x2=2﹣
,x2=2﹣![]() ,
,
∴点Q的坐标为(2+![]() ,﹣
,﹣![]() )或(2﹣
)或(2﹣![]() ,﹣
,﹣![]() );
);
综上,满足条件的点Q有3个:(3,![]() )或(2+
)或(2+![]() ,﹣
,﹣![]() )或(2﹣
)或(2﹣![]() ,﹣
,﹣![]() ).
).


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】根据题意,解答下列问题: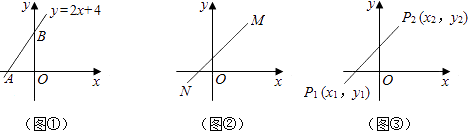
(1)如图①,已知直线y=2x+4与x轴、y轴分别交于A、B两点,求线段AB的长;
(2)如图②,类比(1)的求解过程,请你通过构造直角三角形的方法,求出两点M(3,4),N(﹣2,﹣1)之间的距离;
(3)如图③,P1(x1 , y1),P2(x2 , y2)是平面直角坐标系内的两点,请你利用图③构造直角三角形,并直接写出P1P2的长度(用含有x1 , x2 , y1 , y2的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下列各组线段为边,能组成三角形的是( )
A. 2cm、2cm、4cmB. 2cm、6cm、3cm
C. 8cm、6cm、3cmD. 11cm、4cm、6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD;
(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】位于环水东湾新城区的茂名市第一中学新校区占地面积约为536.5亩.将536.5用科学记数法可表示为( )
A.0.5365×103
B.5.365×102
C.53.65×10
D.536.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com