【题目】一次函数y=2x﹣1一定不经过第________象限．
科目：初中数学 来源： 题型：
【题目】某市有12000名学生参加考试，为了了解考试情况，从中抽取1000名学生的成绩进行统计分析，在这个问题中，有下列三种说法：①1000名考生是总体的一个样本；②每一名考生是个体；③样本容量是1000人．其中正确的说法有（ ）
A. 0种 B. 1种 C. 2种 D. 3种
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】大黄鱼是中国特有的地方性鱼类，有“国鱼”之称，由于过去滥捕等多种因素，大黄鱼资源已基本枯竭，目前，我市已培育出十余种大黄鱼品种，某鱼苗人工养殖基地对其中的四个品种“宁港”、“御龙”、“甬岱”、“象山港”共300尾鱼苗进行成活实验，从中选出成活率最高的品种进行推广，通过实验得知“甬岱”品种鱼苗成活率为
，并把实验数据绘制成下列两幅统计图(部分信息未给出)：
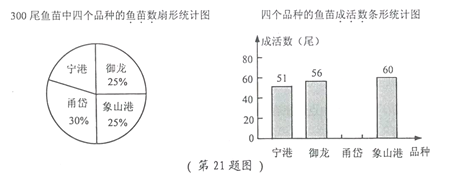
(1) 求实验中“宁港”品种鱼苗的数量；
(2) 求实验中“甬岱”品种鱼苗的成活数，并补全条形统计图；
(3)你认为应选哪一品种进行推广？请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，BC＞AB，∠BAD的平分线AF与BD，BC分别交于点E，F，点O是BD的中点，直线OK∥AF，交AD于点K，交BC于点G．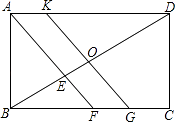
（1）求证：△DOK≌△BOG；
（2）探究线段AB、AK、BG三者之间的关系，并证明你的结论；
（3）若KD=KG，BC=2 
﹣1，求KD的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：如图1，抛物线
与
轴交于A，B两点，点P在抛物线上（点P与A，B两点不重合），如果△ABP的三边满足
，则称点P为抛物线的勾股点。
（1）直接写出抛物线
的勾股点的坐标；
（2）如图2，已知抛物线C：
与
轴交于A，B两点，点P（1，
）是抛物线C的勾股点，求抛物线C的函数表达式；
（3）在（2）的条件下，点Q在抛物线C上，求满足条件
的点Q（异于点P）的坐标
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，借助直角三角板可以找到一元二次方程的实数根．比如对于方程
，操作步骤是：
第一步：根据方程的系数特征，确定一对固定点A（0，1），B（5，2）；
第二步：在坐标平面中移动一个直角三角板，使一条直角边恒过点A，另一条直角边恒过点B；
第三步：在移动过程中，当三角板的直角顶点落在x轴上点C处时，点C的横坐标m即为该方程的一个实数根（如图1）；
第四步：调整三角板直角顶点的位置，当它落在x轴上另一点D处时，点D的横坐标n即为该方程的另一个实数根．
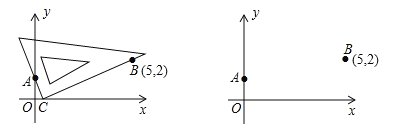
（1）在图2中，按照“第四步”的操作方法作出点D（请保留作出点D时直角三角板两条直角边的痕迹）；
（2）结合图1，请证明“第三步”操作得到的m就是方程的一个实数根；
（3）上述操作的关键是确定两个固定点的位置，若要以此方法找到一元二次方程
（a≠0，
≥0）的实数根，请你直接写出一对固定点的坐标；
（4）实际上，（3）中的固定点有无数对，一般地，当m1，n1，m2，n2与a，b，c之间满足怎样的关系时，点P（m1，n1），Q（m2，n2）就是符合要求的一对固定点？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
