
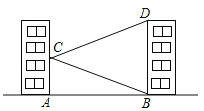
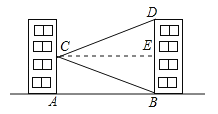
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(1)求∠BCD的度数.
(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)
【答案】(1)38°;(2)20.4m.
【解析】
试题分析:(1)过点C作CE与BD垂直,根据题意确定出所求角度数即可;
(2)在直角三角形CBE中,利用锐角三角函数定义求出BE的长,在直角三角形CDE中,利用锐角三角函数定义求出DE的长,由BE+DE求出BD的长,即为教学楼的高.
试题解析:(1)过点C作CE⊥BD,则有∠DCE=18°,∠BCE=20°,∴∠BCD=∠DCE+∠BCE=18°+20°=38°;
(2)由题意得:CE=AB=30m,在Rt△CBE中,BE=CEtan20°≈10.80m,在Rt△CDE中,DE=CDtan18°≈9.60m,∴教学楼的高BD=BE+DE=10.80+9.60≈20.4m,则教学楼的高约为20.4m.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
【题目】丽水某公司将“丽水山耕”农副产品运往杭州市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:

(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午00之前到达杭州市场?请说明理由;
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线l:y=﹣ ![]() x+
x+ ![]() 分别交x轴,y轴于A,B两点,点C在x轴负半轴上,且∠ACB=30°.
分别交x轴,y轴于A,B两点,点C在x轴负半轴上,且∠ACB=30°.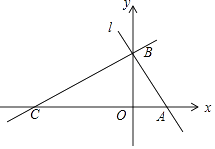
(1)求A,C两点的坐标.
(2)若点M从点C出发,以每秒1个单位长度的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,求出S关于t的函数关系式,并写出自变量的取值范围.
(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A,B,P,Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意,解答下列问题: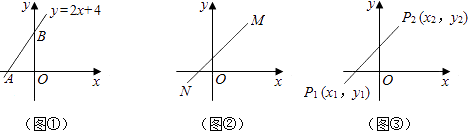
(1)如图①,已知直线y=2x+4与x轴、y轴分别交于A、B两点,求线段AB的长;
(2)如图②,类比(1)的求解过程,请你通过构造直角三角形的方法,求出两点M(3,4),N(﹣2,﹣1)之间的距离;
(3)如图③,P1(x1 , y1),P2(x2 , y2)是平面直角坐标系内的两点,请你利用图③构造直角三角形,并直接写出P1P2的长度(用含有x1 , x2 , y1 , y2的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为 m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD;
(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=4,P是CD边上的动点(P点不与C、D重合),过点P作直线与BC的延长线交于点E,与AD交于点F,且CP=CE,连接DE、BP、BF,设CP═x,△PBF的面积为S1 , △PDE的面积为S2 . 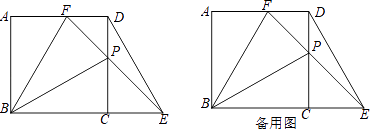
(1)求证:BP⊥DE.
(2)求S1﹣S2关于x的函数解析式,并写出x的取值范围.
(3)分别求当∠PBF=30°和∠PBF=45°时,S1﹣S2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com