
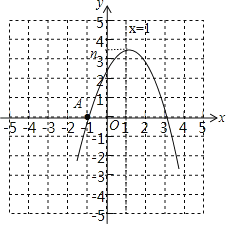
【题目】已知抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),与y轴的交点在(0,2),(0,3)之间(包含端点),顶点坐标为(1,n),则下列结论:
①2a+b<0;
②﹣1≤a≤﹣![]() ;
;
③对于任意实数m,a(m2﹣1)+b(m﹣1)≤0总成立;
④关于x的方程ax2+bx+c=n+1有两个不相等的实数根.
其中结论正确的序号是_____.
【答案】②③.
【解析】
由对称轴、顶点坐标和y轴交点坐标代入可得b=-2a,c=-3a可判断①②,对函数图像得最大值进行分析可以判断③④.
如图,
∵抛物线的顶点坐标为(1,n),
∴抛物线的对称性为直线x=﹣![]() =1,
=1,
∴b=﹣2a,
∴2a+b=0,所以①错误;
∵抛物线与x轴交于点A(﹣1,0),
∴a﹣b+c=0,
∴c=b﹣a=﹣2a﹣a=﹣3a,
∵抛物线与y轴的交点在(0,2),(0,3)之间(包含端点),
∴2≤c≤3,即2≤﹣3a≤3,
∴﹣1≤a≤﹣![]() ,所以②正确;
,所以②正确;
∵当x=1时,y有最大值,
∴a+b+c≥am2+bm+c(m为任意实数),
即a(m2﹣1)+b(m﹣1)≤0,所以③正确;
∵抛物线的顶点坐标为(1,n),
∴直线y=n与抛物线只有一个交点,
∴直线y=n+1与抛物线没有公共点,
∴关于x的方程ax2+bx+c=n+1没有实数根,所以④错误.
故答案为②③.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】某商店销售一种商品,童威经市场调查发现:该商品的周销售量![]() (件)是售价
(件)是售价![]() (元/件)的一次函数,其售价、周销售量、周销售利润
(元/件)的一次函数,其售价、周销售量、周销售利润![]() (元)的三组对应值如下表:
(元)的三组对应值如下表:
售价 | 50 | 60 | 80 |
周销售量 | 100 | 80 | 40 |
周销售利润 | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价-进价)
(1)①求![]() 关于
关于![]() 的函数解析式(不要求写出自变量的取值范围)
的函数解析式(不要求写出自变量的取值范围)
②该商品进价是_________元/件;当售价是________元/件时,周销售利润最大,最大利润是__________元
(2)由于某种原因,该商品进价提高了![]() 元/件
元/件![]() ,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求
,物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板Rt△ABD与Rt△ACB(其中∠ABD=∠ACB=90°,∠D=60°,∠ABC=45°)如图摆放,Rt△ABD中∠D所对的直角边与Rt△ACB的斜边恰好重合.以AB为直径的圆经过点C,且与AD相交于点E,连接EB,连接CE并延长交BD于F.
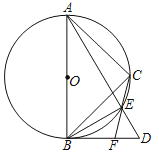
(1)求证:EF平分∠BED;
(2)求△BEF与△DEF的面积的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
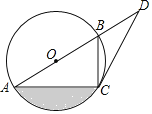
【题目】如图,已知AB是⊙O上的点,C是⊙O上的点,点D在AB的延长线上,∠BCD=∠BAC.
(1)求证:CD是⊙O的切线;
(2)若∠D=30°,BD=2,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知坐标平面上有一顶点为![]() 的抛物线,
的抛物线,![]() 点坐标为
点坐标为![]() ,则可设此抛物线的顶点式为______;若此抛物线又与直线
,则可设此抛物线的顶点式为______;若此抛物线又与直线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() 为正三角形,则可求得此抛物线与
为正三角形,则可求得此抛物线与![]() 轴的交点坐标为________________
轴的交点坐标为________________
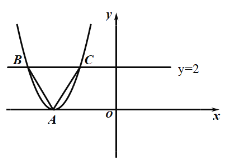
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (k≠0,x>0)的图象与直线y=4x相交于点C,过直线上点A(2,a)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=4BD.
(k≠0,x>0)的图象与直线y=4x相交于点C,过直线上点A(2,a)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=4BD.
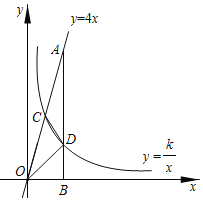
(1)求a的值;
(2)求k的值;
(3)连接OD,CD,求△OCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药公司有A仓、B仓两个原材料仓库和甲、乙两个加工厂,其中A合、B仓共原材料22000吨,从A仓、B仓运往甲加工厂、乙加工厂的运费价如下表:

若将A仓的原材全部运往乙加T所需的费用与B仓的原材料全部运往甲加厂所需费用相同,
(1)A仓、B仓各有原材料多少吨?
(2)若甲加工厂需要从A、B两仓调运9000吨原材料,乙加工厂需要从A、B两仓调运13000原材料,且从A仓运送到甲加工厂的原材料最多9000吨,请问医药公司怎么调运可使总运费最少?求出最少运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表中给出了变量x与ax2,ax2+bx+c之间的部分对应值(表格中的符号“…”表示该项数据已经丢失)
x | -1 | 0 | 1 |
ax | … | … | 1 |
ax+ bx + c | 7 | 2 | … |
(1)写出这条抛物线的开口方向,顶点D的坐标;并说明它的变化情况;
(2)抛物线![]() 的顶点为D,与y轴的交点为A,点M是抛物线对称轴上的一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求点B的坐标:
的顶点为D,与y轴的交点为A,点M是抛物线对称轴上的一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求点B的坐标:
(3)在(2)的条件下,设线段BD交x轴于点C,试写出∠BAD与∠DCO的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
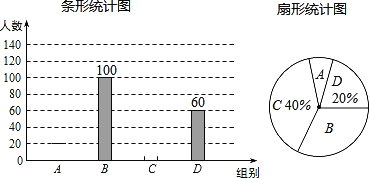
【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,今年受“新冠肺炎”疫情的影响,为落实教育部“停课不停学”的要求,我市中学生进行居家线上学习,为保证广大学生的身心健康,有关部门就“你每天线上学习时在室内或室外安全区域体育锻炼时间是多少”的问题在某校开展了电话调查,随机抽查了部分学生,再根据锻炼时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如图两幅不完整统计图,请根据图中信息回答问题:
(1)此次抽查的学生数为 人,并补全条形统计图;
(2)计算扇形统计图中A组部分所对应的扇形圆心角度数;
(3)若当天该校进行居家线上学习的学生数为1300人,请估计在当天达到国家规定体育活动时间的学生有多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com