练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

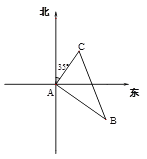
    【题目】如图，甲、乙两船从港口A同时出发，甲船以每小时30海里的速度向北偏东35°方向航行，乙船以每小时40海里的速度向另一方向航行，1小时后，甲船到达C岛，乙船达到B岛，若C、B两岛相距50海里，则乙船的航行方向为南偏东多少度？

    【答案】55°

    【解析】

    首先计算出甲乙两船的路程，再根据勾股定理逆定理可证明∠BAC=90°，然后再根据C岛在A北偏东35°方向，可得B岛在A南偏东55°方向．

    由题意得：甲1小时的路程：AC=30×1=30海里，

    乙1小时的路程：AC=40×1=40海里，
    ∵302+402=502，

    即=+
    ∴∠BAC=90°，
    ∵C岛在A北偏东35°方向，
    ∴B岛在A南偏东55°方向．
    ∴乙船航行的角度是南偏东55°方向．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】应用我们学过的数学知识,解决下列问题:

    (1)如图①,从教学楼到图书馆,总有少数同学不走人行道而横穿草坪,解释这一不文明现象用到的基本事实是__________.

    (2)如图②,我们学过用直尺和三角尺画平行线的方法,如图所示,直线根据的基本事实是__________.

    (3)如图③,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,解释这一实际应用的基本事实是___________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将抛物线 先向右平移3个单位长度，再向上平移2个单位长度后得到新的抛物线的顶点坐标为 .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的三个顶点A、B、D分别在长方形 EFGH的边EF、FG、EH上，且C到HG的距离是1，到点H，G的距离分别为，，则正方形ABCD的面积为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（数学阅读）

    如图1，在△ABC中，AB＝AC，点P为边BC上的任意一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D，E，过点C作CF⊥AB，垂足为F，求证：PD＋PE＝CF．

    小尧的证明思路是：如图2，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD＋PE＝CF．

    （推广延伸）

    如图3，当点P在BC延长线上时，其余条件不变，请运用上述解答中所积累的经验和方法，猜想PD，PE与CF的数量关系，并证明．

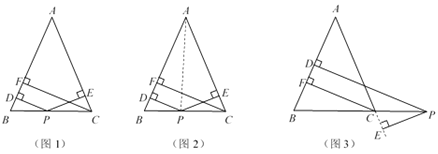
    （解决问题）

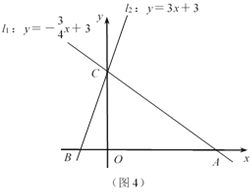
    如图4，在平面直角坐标系中有两条直线l1：y＝－x＋3，l2：y＝3x＋3，l1，l2与x轴的交点分别为A，B．

    (1)两条直线的交点C的坐标为 ；

    (2)说明△ABC是等腰三角形；

    (3)若l2上的一点M到l1的距离是1，运用上面的结论，求点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两车从A城出发沿一条笔直公路匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示．

    （1）A，B两城相距 千米，乙车比甲车早到 小时；

    （2）甲车出发多长时间与乙车相遇？

    （3）若两车相距不超过20千米时可以通过无线电相互通话，则两车都在行驶过程中可以通过无线电通话的时间有多长？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点，DE⊥DF，交AB于点E，连结EG、EF．

    （1）求证：BG＝CF．

    （2）请你判断BE+CF与EF的大小关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，长方形纸片ABCD的长AD＝9cm，宽AB＝3cm，将其折叠，使点D与点B重合．

    求：（1）折叠后DE的长；（2）以折痕EF为边的正方形面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，如图，在R t△ABC中，∠C＝90°，∠BAC的角平分线AD交BC边于D．

    （1）动手操作：利用尺规作，以AB边上一点O为圆心，过A，D两点作⊙O，与AB的另一个交点为E，与AC的另一个交点为F（不写作法，保留作图痕迹），再判断直线BC与⊙O的位置关系，并说明理由。
    （2）若∠BAC=60度，CD= ，求线段BD、BE与劣弧DE所围成的图形面积．（结果保留根号和 ）

    查看答案和解析>>

    同步练习册答案