
����Ŀ������ѧ�Ķ���
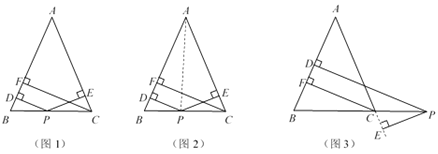
��ͼ1������ABC�У�AB��AC����PΪ��BC�ϵ�����һ�㣬����P��PD��AB��PE��AC������ֱ�ΪD��E������C��CF��AB������ΪF����֤��PD��PE��CF��
СҢ��֤��˼·������ͼ2������AP������ABP����ACP���֮�͵�����ABC���������֤����PD��PE��CF��
���ƹ�������
��ͼ3������P��BC�ӳ�����ʱ�������������䣬��������������������۵ľ���ͷ���������PD��PE��CF��������ϵ����֤����
�����������
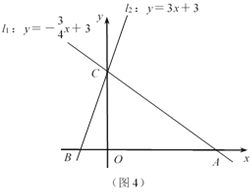
��ͼ4����ƽ��ֱ������ϵ��������ֱ��l1��y����![]() x��3��l2��y��3x��3��l1��l2��x��Ľ���ֱ�ΪA��B��
x��3��l2��y��3x��3��l1��l2��x��Ľ���ֱ�ΪA��B��
(1)����ֱ�ߵĽ���C������Ϊ ��
(2)˵����ABC�ǵ��������Σ�
(3)��l2�ϵ�һ��M��l1�ľ�����1����������Ľ��ۣ����M�����꣮
���𰸡����ƹ����������룺PD��PE��CF��֤���������������������(1)C(0��3)��(2)֤����������(3)M(��![]() ��2)��M(
��2)��M(![]() ��4)��
��4)��
��������
���ƹ��������������⣬���룺PD��PE��CF,��S��APB��S��ACP��S��ABC��������. �����������(1)����ֱ���ཻ֪�����������飬�õ�C������; (2)���ݷ����齫A,B���������AB�߶γ����ɹ��ɶ�����AC�߶γ�������֤����ABC�ǵ��������Σ���3�������������۵�ME�߶γ����ɴ˵õ�M�������.
�ƹ�����
���룺PD��PE��CF��
֤������ͼ������AP��
�� S��APB��S��ACP��S��ABC����
�� ![]() AB��PD��
AB��PD��![]() AC��PE��
AC��PE��![]() AB��CF��
AB��CF��
�� AB��AC��
�� PD��PE��CF��
�������
(1)C(0��3)��
(2)l1��y����![]() x��3����y��0����x��4����A(4��0)��
x��3����y��0����x��4����A(4��0)��
l2��y��3x��3����y��0����x����1����B(��1��0)��
�� AB��5��
��Rt��AOC�У���AOC��90�㣬
�� AC2��AO2��CO2 ����AC��5��
�� AB��AC��5���� ��ABC�ǵ�����������
(3)��M��ֱ���MD��AC��ME��AB������ֱ�ΪD��E��
������Ľ��۵ã�ME��MD��CO��ME��MD��CO��
�� ME��2��ME��4���� M(��![]() ��2)��M(
��2)��M(![]() ��4)��
��4)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У�AF��CE�ֱ��ǡ�BAD�͡�BCD�Ľ�ƽ���ߣ��������е�ͼ�Σ�������һ��������ʹ�ı���AECFΪ���Σ������ӵ�һ������������__________����ֻ��д��һ�����ɣ�ͼ�в��������ӱ������������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ֱ��a ��b��ֱ��c���أ��ָ�����������������
�١�2����6 �ڡ�2����8 �ۡ�1����4��180�� �ܡ�3����8���������ж���a��b������������ǣ� ��
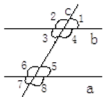
A. �٢� B. �٢� C. �٢� D. �ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��D��BC������һ�㣬����D�ֱ���AB��AC�����ߣ�����ֱ�Ϊ��E��F.
(1)��ͼ�٣�����D��BC��ʲôλ��ʱ��DE��DF����֤����
(2)�������һ�ʵ������£�����AD����ʱͼ�й��м���ȫ�������Σ���д�����е�ȫ��������(����֤��)��
(3)��ͼ�ڣ�����C��AB���ϵĸ�CG������DE��DF��CG�ij�֮����������ĵ�����ϵ��������֤����


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��C��D��AB�Ĵ�ֱƽ���������㣬�ӳ�AC��DB���ڵ�E��AF��BC��DE�ڵ�F��
��֤��(1)AB����CAF�Ľ�ƽ������
(2)��FAD �� ��E��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
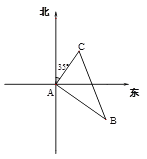
����Ŀ����ͼ���ס��������Ӹۿ�Aͬʱ�������״���ÿСʱ30������ٶ���ƫ��35�㷽���У��Ҵ���ÿСʱ40������ٶ�����һ�����У�1Сʱ�״�����C�����Ҵ��ﵽB������C��B�������50������Ҵ��ĺ��з���Ϊ��ƫ�����ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
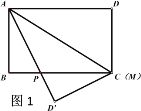
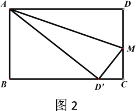
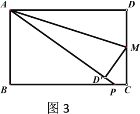
����Ŀ����֪������ABCD�У�AD=10cm,AB=6cm,��M�ڱ�CD�ϣ���C��D�˶����ٶ�Ϊ1cm/s���˶�ʱ��Ϊt�룬����ADM����AM��������ADM����D��Ӧ��ΪD��AD����ֱ�����BC���ڵ�P.
��1����ͼ1����t=0ʱ����֤��PA=PC��
��2����ͼ2����tΪ��ֵʱ����Dǡ�����ڱ�BC�ϣ�
��3����ͼ3����t=3ʱ����CP�ij�.
 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵�����һ�����۳ɱ�Ϊ40Ԫ/ǧ�˵�ˮ��Ʒ���� 50Ԫ /ǧ�����ۣ�һ���¿��۳�500ǧ�ˣ����ۼ�ÿ�Ǽ�1Ԫ�����������ͼ���10ǧ�ˣ�
��1��д������������y����λ��Ԫ�� ���ۼ�x����λ��Ԫ/ǧ�ˣ� ֮��ĺ�������ʽ��
��2�����ۼ۶�Ϊ����ʱ���������������������
��3���̵����������۳ɱ�������10000Ԫ������£�ʹ����������ﵽ8000Ԫ���۵���Ӧ��Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ҫ���������⣮
��1���벹ȫ������ʽ��2x2��4x��0�Ľ⼯�Ĺ��̣�
�ٹ��캯��������ͼ���ݲ���ʽ����������κ���y=��2x2��4x���������������ϵ�У�ͼ1���������κ���y=��2x2��4x��ͼ��ֻ����ͼ�ɣ���
����ý�㣬��ʾ���裬��y=0ʱ����÷��̩�2x2��4x=0�Ľ�Ϊ�� �������þ���߱�ʾ������y=��2x2��4xͼ����y��0�IJ��֣�
�۽���ͼ��д���⼯��������ʾͼ�ɵò���ʽ��2x2��4x��0�Ľ⼯Ϊ��2��x��0����������������һԪһ�β���ʽ�⼯�Ĺ��̣���ʽx2��2x+1��4�Ľ⼯��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com