
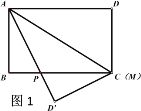
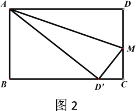
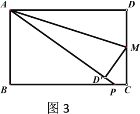
【题目】已知长方形ABCD中,AD=10cm,AB=6cm,点M在边CD上,由C往D运动,速度为1cm/s,运动时间为t秒,将△ADM沿着AM翻折至△ADM,点D对应点为D,AD所在直线与边BC交于点P.
(1)如图1,当t=0时,求证:PA=PC;
(2)如图2,当t为何值时,点D恰好落在边BC上;
(3)如图3,当t=3时,求CP的长.
 (
(
【答案】(1)见解析(2)![]() (3)
(3)![]()
【解析】
(1)由折叠性质可得![]() ADC
ADC![]() A DC可得∠DAC=∠DAC, 在长方形ABCD中,AD//BC,可得 ∠DAC=∠BCA,从而得到∠DAC=∠BCA,即可得出结论。
A DC可得∠DAC=∠DAC, 在长方形ABCD中,AD//BC,可得 ∠DAC=∠BCA,从而得到∠DAC=∠BCA,即可得出结论。
(2)由折叠性质可得![]() ADC
ADC![]() A DC可得DM=DM=6-t,AD=A D=10,根据勾股定理可得B D=8则C D=2,在Rt
A DC可得DM=DM=6-t,AD=A D=10,根据勾股定理可得B D=8则C D=2,在Rt![]() CM D中,根据勾股定理列出方程即可。
CM D中,根据勾股定理列出方程即可。
(3)当t=3时,CM=DM=3, 连接PM,根据HL证得![]() M DP
M DP![]() MCP,可得DP=PC, ∠DMP=∠CMP, 由折叠性质可得得出∠AMD=∠AMD,从而证得∠AMP=90
MCP,可得DP=PC, ∠DMP=∠CMP, 由折叠性质可得得出∠AMD=∠AMD,从而证得∠AMP=90![]() ,再根据
,再根据![]() ADM
ADM![]() MDP即可。
MDP即可。
(1)当t=0时,M与C重合
由折叠性质可得![]() ADC
ADC![]() A DC
A DC
∴∠DAC=∠DAC,
在长方形ABCD中,AD//BC,
∴ ∠DAC=∠BCA
∴∠DAC=∠BCA,
∴PA=PC;
(2)由折叠性质可得![]() ADC
ADC![]() A DC
A DC
∴DM=DM=6-t,AD=A D=10,
在Rt![]() ABD中,B D=
ABD中,B D=![]() =8
=8
∴DC=BC- B D=10-8=2cm
在Rt![]() CMD中,
CMD中,
∴![]()
解得:t=![]()
∴当t=![]() 时,点D恰好落在边BC上;
时,点D恰好落在边BC上;
(3)当t=3时,CM=DM= DM=3,
由折叠性质可得:∠ADM=∠D=90![]()

连接PM,
在Rt![]() M DP和Rt
M DP和Rt![]() MCP中
MCP中
![]()
∴![]() M DP
M DP![]() MCP,
MCP,
∴DP=PC, ∠DMP=∠CMP,
∵∠AMD=∠AMD
∴∠PMD+∠AMD=90![]()
∵∠MAP +∠AMD=90![]()
∴∠PMD=∠MAP
∵∠ADM=∠PDM
∴![]() M DA
M DA![]() P DM
P DM
∴![]()
∴![]() = P D. A D
= P D. A D
∴![]() = P D.10
= P D.10
∴P D=![]()
∴CP=![]()


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形ECGF都是正方形,点C、D、E在一条直线上,点B、C、G在一条直线上.
(1)写出表示阴影部分面积的表达式(结果要求化简);
(2)当![]() 求阴影面积的面积
求阴影面积的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A、F的直线垂直平分线段BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(数学阅读)
如图1,在△ABC中,AB=AC,点P为边BC上的任意一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D,E,过点C作CF⊥AB,垂足为F,求证:PD+PE=CF.
小尧的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
(推广延伸)
如图3,当点P在BC延长线上时,其余条件不变,请运用上述解答中所积累的经验和方法,猜想PD,PE与CF的数量关系,并证明.
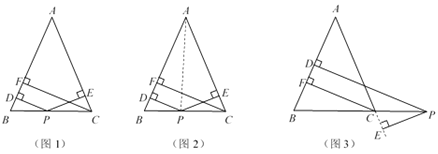
(解决问题)
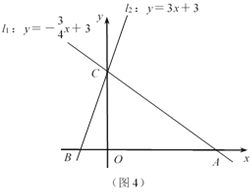
如图4,在平面直角坐标系中有两条直线l1:y=-![]() x+3,l2:y=3x+3,l1,l2与x轴的交点分别为A,B.
x+3,l2:y=3x+3,l1,l2与x轴的交点分别为A,B.
(1)两条直线的交点C的坐标为 ;
(2)说明△ABC是等腰三角形;
(3)若l2上的一点M到l1的距离是1,运用上面的结论,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的切线,B为切点,AO的延长线交⊙O于点C,连接BC,如果∠A=30°,AB=2 ![]() ,那么AC的长等于( )
,那么AC的长等于( )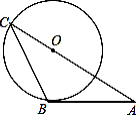
A.4
B.6
C.4 ![]()
D.6 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com