练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图,四边形ABCD和四边形ECGF都是正方形,点C、D、E在一条直线上,点B、C、G在一条直线上.

    (1)写出表示阴影部分面积的表达式(结果要求化简)；

    (2)当求阴影面积的面积

    【答案】（1）a23a+18;

    （2）14．

    【解析】

    （1）阴影部分的面积等于两个正方形的面积之和减去△ABD和△ BGF的面积，然后分别计算即可；

    （2）把a=4代入（1）中所求的表达式，求值即可.

    （1）∵S□ABCD+S□ECGF=a2+62，S△ABD=×a2，S△BGF=×（a+6）×6=3（a+6）

    ∴S阴影= S□ABCD+S□ECGF S△ABD S△BGF=a2+363（a+6）=a23a+18;

    （2）当a=4时，S阴影=a23a+18=×423×4+18=14.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】【概念学习】

    规定：求若干个相同的有理数（均不等）的除法运算叫做除方，如2÷2÷2， 等.类比有理数的乘方，我们把记作，读作“的圈次方”， 记作，读作“的圈次方”.一般地，把（）记作读作“的圈次方”

    【初步探究】

    （1）直接写出计算结果： =_____， _____

    （2）关于除方，下列说法错误的是（______）

    A.任何非零数的圈2次方都等于1

    B.对于任何正整数，

    C.

    D.负数的圈奇数次方结果是负数，负数的圈偶数次方结果是正数

    【深入思考】

    我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘法运算呢？

    （3）试一试：仿照上面的算式，将下列运算结果直接写成幂的形式=_________

    （4）想一想：将一个非零有理数的圈n次方写成幂的形式等于_________

    （5）算一算：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知数轴上的点A和点B之间的距离为28个单位长度，点A在原点左边，距离原点8个单位长度，点B在原点的右边．

    （1）请直接写出A，B两点所对应的数．

    （2）数轴上点A以每秒1个单位长度的速度出发向左运动，同时点B以每秒3个单位长度的速度出发向左运动，在点C处追上了点A，求C点对应的数．

    （3）已知，数轴上点M从点A向左出发，速度为每秒1个单位长度，同时点N从点B向左出发，速度为每秒2个单位长度，经t秒后点M、N、O（O为原点）其中的一点恰好到另外两点的距离相等，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD中，AF、CE分别是∠BAD和∠BCD的角平分线，根据现有的图形，请添加一个条件，使四边形AECF为菱形，则添加的一个条件可以是__________．（只需写出一个即可，图中不能再添加别的“点”和“线”）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①,线段AB=8cm,点C为线段AB上的一个动点(点C不与点A、B重合),D、E分别是线段AC和线段BC的中点.

    (1)求DE的长；

    (2)知识迁移:如图②,已知∠AOB=,射线OC在∠AOB的内部,若OD、OE分别平分∠AOC和∠BOC,求∠DOE的度数(用含的代数式表示).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，所有小正方形的边长都为1，A、B、C都在格点上．

    （1）过点C画直线AB的平行线（不写作法，下同）；

    （2）过点A画直线BC的垂线，并注明垂足为G；过点A画直线AB的垂线，交BC于点H．

    （3）线段　 　的长度是点A到直线BC的距离，线段AH的长度是点　 　到直线　 　的距离．

    （4）因为直线外一点到直线上各点连接的所有线中，垂线段最短，所以线段AG、AH的大小关系为AG　 　AH．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将一张正方形纸片，剪成四个大小形状一样的小正方形，然后将其中的一个小正方形再按同样的方法剪成四个小正方形，再将其中的一个小正方形剪成四个小正方形，如此循环进行下去．

    （1）填出下表：

    剪的次数

    1

    2

    3

    4

    5

    6

    正方形个数

    （2）如果剪了100次，共剪出　 　个小正方形？

    （3）如果剪次，共剪出　 　个小正方形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，直线a 、b被直线c所截，现给出下列四种条件：

    ①∠2＝∠6 ②∠2＝∠8 ③∠1＋∠4＝180° ④∠3＝∠8，其中能判断是a∥b的条件的序号是（ ）

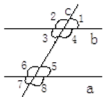
    A. ①② B. ①③ C. ①④ D. ③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

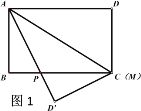
    【题目】已知长方形ABCD中，AD=10cm,AB=6cm,点M在边CD上，由C往D运动，速度为1cm/s，运动时间为t秒，将△ADM沿着AM翻折至△ADM，点D对应点为D，AD所在直线与边BC交于点P.

    （1）如图1，当t=0时，求证：PA=PC；

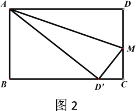
    （2）如图2，当t为何值时，点D恰好落在边BC上；

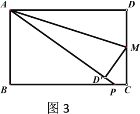
    （3）如图3，当t=3时，求CP的长.

    （

    查看答案和解析>>

    同步练习册答案