
【题目】已知数轴上的点A和点B之间的距离为28个单位长度,点A在原点左边,距离原点8个单位长度,点B在原点的右边.
(1)请直接写出A,B两点所对应的数.
(2)数轴上点A以每秒1个单位长度的速度出发向左运动,同时点B以每秒3个单位长度的速度出发向左运动,在点C处追上了点A,求C点对应的数.
(3)已知,数轴上点M从点A向左出发,速度为每秒1个单位长度,同时点N从点B向左出发,速度为每秒2个单位长度,经t秒后点M、N、O(O为原点)其中的一点恰好到另外两点的距离相等,求t的值.
【答案】(1)A点所对应的数是﹣8;B对应的数是20;(2)C对应的数为﹣22;(3)t的值为4或10或16或28.
【解析】
(1)根据题意找出A与B点对应的数即可;
(2)设经过x秒点A、B相遇,根据题意列出方程,求出方程的解得到x的值,即可确定出C点对应的数;
(3)根据题意列出关于t的方程,求出方程的解即可得到结果.
解:(1)根据题意得:A点所对应的数是﹣8;B对应的数是20;
(2)设经过x秒点A、B相遇,
根据题意得:3x﹣x=28,
解得:x=14,
则点C对应的数为﹣8﹣14=﹣22;
(3)依题意有:
20﹣2t=8+t,
解得t=4;
或2t=20,
解得t=10;
或2(2t﹣20)=8+t,
解得t=16;
或2t﹣t=20+8,
解得t=28;
或2t﹣20=2(8+t),方程无解.
故t的值为4或10或16或28.
![]()
故答案为:(1)A点所对应的数是﹣8;B对应的数是20;(2)﹣22;(3)4或10或16或28.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AC⊥BC于C,CD⊥AB于D,点E在AC上,EF⊥AB于F,且∠1=∠2.
(1)试判断CD与EF是否平行并说明理由.
(2)试判断DG与BC是否垂直并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形AOB和三角形COD中,∠AOB=∠COD,
(1)已知∠AOB=90°,把两个三角形拼成如图①所示的图案,当∠BOD=30°时,求∠AOC的度数.
(2)已知∠AOB=90°,把两个三角形拼成如图②所示的图案,当∠AOC=2∠BOD时,求∠BOD的度数.
(3)当∠AOB=α时,把两个三角形拼成如图③所示的图案.用含有α的代数式表示∠AOC+∠BOD.

查看答案和解析>>
科目:初中数学 来源: 题型:
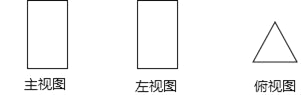
【题目】已知如图为一几何体的三视图:主视图和左视图都是长方形,俯视图是等边三角形
(1)写出这个几何体的名称;
(2)若主视图的高为10cm,俯视图中三角形的边长为4cm,求这个几何体的侧面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第2次从点A1向右移动6个单位长度到达点A2,第3次从点A2向左移动9个单位长度到达点A3,…,按照这种移动规律进行下去,第n次移动到达点An,如果点An与原点的距离不小于50,那么n的最小值是_____.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=CD,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,若DE=BF,则下列结论:①CF=AE;②OE=OF;③四边形ABCD是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是
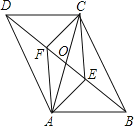
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、M两点,若点M的坐标是(-4,-2),则点N的坐标为( )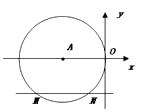
A.(-1,-2)
B.(1,2)
C.(-1.5,-2)
D.(1.5,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形ECGF都是正方形,点C、D、E在一条直线上,点B、C、G在一条直线上.
(1)写出表示阴影部分面积的表达式(结果要求化简);
(2)当![]() 求阴影面积的面积
求阴影面积的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A、F的直线垂直平分线段BC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com