Question

【题目】如图，已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，在直线l3上有点P（点P与点C、D不重合），点A在直线l1上，点B在直线l2上。

（1）如果点P在C、D之间运动时，试说明∠1+∠3=∠2；

（2）如果点P在直线l1的上方运动时，试探索∠1，∠2，∠3之间的关系又是如何？

（3）如果点P在直线l2的下方运动时，试探索∠PAC，∠PBD，∠APB之间的关系又是如何？ （直接写出结论）

Answer 1

【答案】（1）证明见解析（2）当点P在线段DC的延长线上时，∠2=∠3-∠1（3）∠APB+∠PBD=∠PAC

【解析】分析：（1）过点P作PE∥l1，根据l1∥l2可知PE∥l2，根据平行线的性质可得出∠1=∠APE，∠3=∠BPE．再由∠2=∠APE+∠BPE即可得出结论；

（2）如图2所示，当点P在直线l1的上方运动时，∠2=∠3-∠1，过点P作PF∥l1，根据l1∥l2可知PE∥l2，根据平行线的性质可得出∠FPA=∠1，∠FPB=∠3， 即可得∠2=∠FPB-∠PFA=∠3-∠1；（3）∠APB+∠PBD=∠PAC，类比（2）的方法证明即可．

详解：

（1）证明：如图1，过点P作PE∥l1，

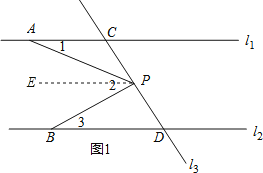
∵l1∥l2，

∴PE∥l2，

∴∠1=∠APE，∠3=∠BPE．

又∵∠2=∠APE+∠BPE，

∴∠2=∠1+∠3；

（2）如图2所示，当点P在直线l1的上方运动时，∠2=∠3-∠1．

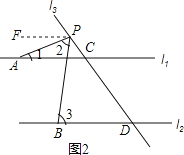
理由：过点P作PF∥l1，

∠FPA=∠1．

∵l1∥l2，

∴PF∥l2，

∴∠FPB=∠3，

∴∠2=∠FPB-∠PFA=∠3-∠1；

（3）∠APB+∠PBD=∠PAC，

理由：如图3所示，点P在直线l2的下方运动时，∠APB+∠PBD=∠PAC．

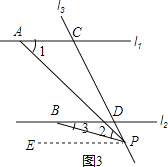
理由：过点P作PE∥l2，∠EPB=∠3．

∵l1∥l2，

∴PE∥l1，

∴∠EPA=∠1，

∴∠2=∠EPA-∠EPB=∠1-∠3．

即∠APB+∠PBD=∠PAC.