
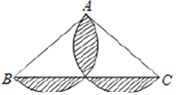
【题目】如图,在△ABC中,AB=AC,AB=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是为________________.
【答案】![]()
【解析】设半圆与底边的交点是D,连接AD.根据直径所对的圆周角是直角,得到AD⊥BC,再根据等腰三角形的三线合一,得到BD=CD=6,根据勾股定理即可求得AD的长,则阴影部分的面积是以AB为直径的圆的面积减去三角形ABC的面积.
解:设半圆与底边的交点是D,连接AD.
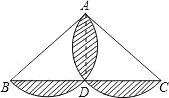
∵AB是直径,∴AD⊥BC.
又∵AB=AC,∴BD=CD=6.
根据勾股定理,得
AD=![]() =2
=2![]() .
.
∵阴影部分的面积的一半=以AB为直径的半圆的面积-三角形ABD的面积
=以AC为直径的半圆的面积-三角形ACD的面积,
∴阴影部分的面积=以AB为直径的圆的面积-三角形ABC的面积
=16π![]() ×12×2
×12×2![]() =16π-12
=16π-12![]() .
.
故答案为:16π-12![]() .
.
“点睛”此题综合运用了圆周角定理的推论、等腰三角形的三线合一、勾股定理、圆面积公式和三角形的面积公式.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】已知一个多项式与2x2﹣3x﹣1的和等于x2﹣2x﹣3,则这个多项式是( )
A.﹣x2+2x+2
B.﹣x2+x+2
C.x2﹣x+2
D.﹣x2+x﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①35=3×3×3×3×3;②﹣1是单项式,且它的次数为1;③若∠1=90°﹣∠2,则∠1与∠2互为余角;④对于有理数n、x、y(其中xy≠0),若 ![]() =
= ![]() ,则x=y.其中不正确的有( )
,则x=y.其中不正确的有( )
A.3个
B.2个
C.1个
D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a,b,c是直角三角形的三条边长,斜边c上的高的长是h , 给出下列结论:
①以a2 , b2 , c2的长为边的三条线段能组成一个三角形;②以 ![]() ,
, ![]() ,
, ![]() 的长为边的三条线段能组成一个三角形;③以a+b , c+h , h的长为边的三条线段能组成直角三角形;④以
的长为边的三条线段能组成一个三角形;③以a+b , c+h , h的长为边的三条线段能组成直角三角形;④以 ![]() ,
, ![]() ,
, ![]() 的长为边的三条线段能组成直角三角形,正确结论的序号为 .
的长为边的三条线段能组成直角三角形,正确结论的序号为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com