
����Ŀ��Ϊ�˽ⱾУ���꼶ѧ����ĩ��ѧ���������С���ھ��꼶�����ȡ��һ����ѧ������ĩ��ѧ�ɼ�Ϊ��������ΪA��100��90�֣���B��89��80�֣���C��79��60�֣���D��59��0�֣��ĸ��ȼ�����ͳ�ƣ�����ͳ�ƽ�����Ƴ�����ͳ��ͼ���������ͳ��ͼ����������⣺
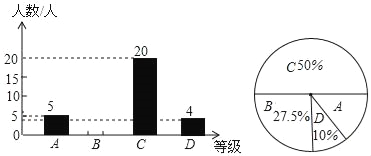
��1����������ȡ��ѧ�����ж����ˣ�
��2���벹ȫ����ͳ��ͼ��
��3�����ѧУ���꼶����ѧ��1200�ˣ�������Ϊ80�֣���80�֣�����Ϊ���㣬�������ξ��꼶ѧ����ĩ��ѧ���Գɼ�Ϊ�����ѧ��������Լ�ж��٣�
���𰸡���1��40������2������������3��480��
��������
���⣨1�������������C����ռ�ı���Ϊ50%����������=ij�������±��������㣻
��2������������ȥA��C��D���������B�ȵ��������ٲ�ȫ����ͳ��ͼ��
��3���������������壮��������1200���������в��Գɼ��ȼ���80�֣���80�֣����ϵ�ѧ����ռ�ٷֱȼ��ɣ�
����������⣺��1����������ȡ��ѧ�����У�20��50%=40���ˣ���
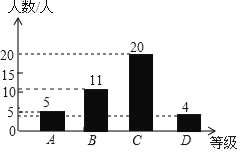
��2��B�ȼ��������ǣ�40��27.5%=11�ˣ���ͼ��
��3����������ã�![]() ��1200=480���ˣ���
��1200=480���ˣ���
����ξ��꼶ѧ����ĩ��ѧ���Գɼ�Ϊ�����ѧ��������Լ��480��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
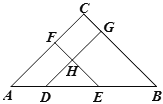
����Ŀ����ͼ���ڡ�ABC�� ����A=��B��D��E�DZ�AB�ϵĵ㣬DG��AC��EF��BC��DG��EF�� ���ڵ�H��
(1)��HDE���HED�Ƿ���ȣ���˵�����ɣ�
��:��HDE=��HED���������£�
��DG��AC(��֪)
���� �������� ���� �� ���� ���� ������
�� EF��BC (��֪)
������ ������ ���� �� �� ����
�֡ߡ�A=��B (��֪)
�� �� �� ��.
(2)�����C=90�㣬DG�� EF�к�λ�ù�ϵ�������� (1)�еĽ��˵�����ɣ�
�⣺�������������������������£�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ר��������ij���ͺŵ���������֪���ͺ������Ľ���Ϊ10��Ԫ/��������һ��ʱ����֣������ͺ������ۼ۶�Ϊ15��Ԫ/��ʱ��ƽ��ÿ���۳�8�����ۼ�ÿ����0.5��Ԫ��ƽ��ÿ�ܶ��۳�2����
��1����Ҫƽ��ÿ���۳�����������15�������������ۼ���ඨΪ������Ԫ��
��2���õ�ƻ��µ��ۼۣ��������������������ٿ�棬��Ҫȷ��ƽ��ÿ�ܵ���������Ϊ40��Ԫ��ÿ���������ۼ۶�Ϊ���ٺ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˴����л����㴫ͳ�Ļ���ijУѧ������֯��һ��ȫУ1200��ѧ���μӵ���������д������������ɼ���ʤ����
���������в���ѧ���ijɼ���������50�֣�Ϊ�˸��õ��˽Ȿ�δ����ijɼ��ֲ�����������ȡ������100��ѧ���ijɼ���Ϊ���������������õ����в�������ͳ��ͼ����
�ɼ�x/�� | Ƶ�� | Ƶ�� |
50��x��60 | 10 | 0.10 |
60��x��70 | 25 | 0.25 |
70��x��80 | 30 | b |
80��x��90 | a | 0.20 |
90��x��100 | 15 | 0.15 |
�ɼ���70��x��80��һ����ǣ�
70 70 71 71 71 72 72 73 73 73 73 75 75 75 75 76 76 76 76 76 76 76 76 77 77 78 78 78 79 79
�����������Ϣ������������⣺
��1��a���� ����b���� ����
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3����α����ɼ�����λ������ ����
��4������α����ɼ���78�����ϣ���78�֣���ѧ�������ʤ�������У�μ���α�����1200��ѧ���л���ʤ����Լ�ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��![]() ��������
��������![]() �ཻ��A��B���㣬�ҵ�A��1����4��Ϊ�����ߵĶ��㣬��B��x���ϡ�
�ཻ��A��B���㣬�ҵ�A��1����4��Ϊ�����ߵĶ��㣬��B��x���ϡ�
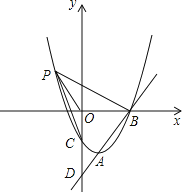
��1���������ߵĽ���ʽ��
��2���ڣ�1���������ߵĵڶ�����ͼ�����Ƿ����һ��P��ʹ��POB����POCȫ�ȣ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��3������Q��y����һ�㣬����ABQΪֱ�������Σ����Q�����ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������F�Ľ���ʽΪ��y��2x2��4nx+2n2+![]() n��nΪʵ����
n��nΪʵ����
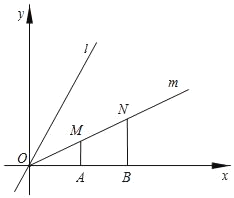
��1����������F��������꣨��n��ʾ������֤������n�仯ʱ������һ����ֱ��l�ϣ�
��2����ͼ������m�ǣ�1����ֱ��l��x��������нǵ�ƽ���ߣ���M��N��������m�ϣ���MA��x�ᡢNB��x�ᣬ����ֱ�Ϊ��A����B����A�ڵ�B��ࣩ����MA+NB��MNʱ�����ж�![]() �Ƿ�Ϊ��ֵ�����ǣ��������ֵ�������ǣ�˵�����ɣ�
�Ƿ�Ϊ��ֵ�����ǣ��������ֵ�������ǣ�˵�����ɣ�
��3����ֱ֪��y��kx+b��������F������һ������أ��ҽصõij��ȶ�Ϊ![]() ��������ֱ�ߵĽ���ʽ��
��������ֱ�ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У��Ե�ABΪֱ���ġ�O�ֱ���AC��BC���ڵ�E��D����BD=CD��
��1����֤����B����C ��
��2������D��DF��OD������F��FH��AB����AB=5��CD=![]() ����AH��ֵ��
����AH��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ���ı���ABCDΪ���Σ���O��AC���е㣬����O��һֱ�߷ֱ���AB��CD���ڵ�E��F������BF��AC�ڵ�M������DE��BO������COB��60����FO��FC�������н��ۣ���FB��OC��OM��CM������EOB�ա�CMB�����ı���EBFD�����Σ���MB��OE��3��2��������ȷ������_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
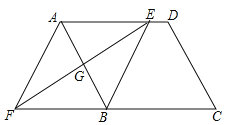
����Ŀ����ͼ����ƽ���ı���ABCD�У���AB�Ĵ�ֱƽ���߽�AD�ڵ�E����CB���ӳ����ڵ�F������AF��BE��
��1����֤����AGE�ա�BGF��
��2�����ж��ı���AFBE����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com