16.问题引入:
在数轴上,一个数所对应的点与原点的距离叫做这个数的绝对值.必然|-2|就表示-2这个点到原点的距离,所以|-2|=2;
问题探究:
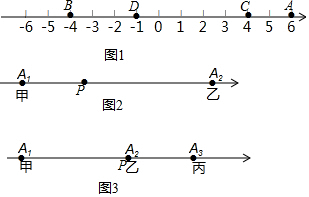
点A、B、C、D所表示的数如图1所示,则A、C两点间的距离为2;B、D两点间的距离为3;
A、B两点间的距离为10;由此,数轴上任意两点E、F分别表示的数是m、n,则E、F两点间的距离可表示为|m-n|.
问题应用:
在一工厂流水线上有依次排列的n个工作台,现要在流水线上设置一个工具台,以方便这n名工人从工作台到工具台拿取工具.为了让工人从工作台到工具台拿工具所走的路程之和最小,我们应该把工具台放在什么位置呢?
为了解决这一问题,我们不妨先从最简单的情形入手:
(1)如图2,若流水线上顺次摆放着2个工作台A
1和A
2,为让2名工人拿工具所走的路程和最小,很明显,工具台P设在A
1和A
2之间的任何地方都行(包括A
1和A
2),因为这时2个工作台上的工人过来取共计所走的距离和等于A
1和A
2之间的距离,要放在其它位置的话,两人所走的距离和都要大于这个距离.
(2)如图3,若流水线上一次摆着3个工作台A
1、A
2和A
3,为让3名工人拿工具所走的路程和最小,应将工具台设在中间工作台A
2处.因为这时3个工作台上工人过来取工具所走的距离和等于A
1和A
3之间的距离,要放在其它位置的话,两人所走的距离和都要大于这个距离.
(3)若流水线上一次摆着4个工作台A
1、A
2、A
3和A
4,为让4名工人拿工具所有的路程和最小,应将工具台设在A
2、A
3之间的任何地方都行(包括A
3和A
2).
(4)若流水线上一次摆放着5个工作台A
1、A
2、A
3、A
4和A
5,为让5名工人拿工具所走的路程和最小,应将工具台设在A
3.
问题拓展:
数轴上三个点1、2、x,那么x在数轴上表示数1,2的点之间(包括1和2)位置时才能到1和2两点的距离和最小,由此,
|x-1|+|x-2|的最小值为1.
根据以上推理方法可求|x-1|+|x-2|+|x-3|+|x-4|+|x-5|的最小值是6,此时x=3.

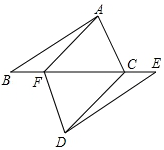 如图,已知△ABF≌△DEC,说明AC∥DF成立的理由.
如图,已知△ABF≌△DEC,说明AC∥DF成立的理由.  阅读快车系列答案
阅读快车系列答案
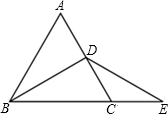 如图,△ABC是等边三角形,BD是中线,延长BC至E,CE=CD,
如图,△ABC是等边三角形,BD是中线,延长BC至E,CE=CD,