
ЁОЬтФПЁПвЛЬѕБЪжБЕФЙЋТЗЩЯгаМзввСНЕиЯрОр2400УзЃЌаЁКьВНааДгМзЕиЕНввЕиЃЌУПЗжжгзп100УзЃЌаЁСњЦяГЕДгввЕиЕНМзЕиКѓанЯЂ2ЗжжгбидТЗдЫйЗЕЛиввЕиЃЎЩшЫћУЧЭЌЪБГіЗЂЃЌдЫЖЏЕФЪБМфЮЊtЃЈЗжЃЉЃЌгыввЕиЕФОрРыЮЊsЃЈУзЃЉЃЌЭМжаЯпЖЮ![]() ЃЌелЯп
ЃЌелЯп![]() ЗжБ№БэЪОСНШЫгыввЕиОрРыsКЭдЫЖЏЪБМфtжЎМфЕФКЏЪ§ЙиЯЕЭМЯѓЃЎ
ЗжБ№БэЪОСНШЫгыввЕиОрРыsКЭдЫЖЏЪБМфtжЎМфЕФКЏЪ§ЙиЯЕЭМЯѓЃЎ

ЃЈ1ЃЉаЁСњЦяГЕЕФЫйЖШЮЊ__________Уз/ЗжжгЃЛ
ЃЈ2ЃЉBЕуЕФзјБъЮЊ__________ЃЛ
ЃЈ3ЃЉаЁСњДгввЕиЦяЭљМзЕиЪБЃЌsгыtжЎМфЕФКЏЪ§БэДяЪНЮЊ__________ЃЛЃЈаДГіtЕФШЁжЕЗЖЮЇЃЉ
ЃЈ4ЃЉаЁКьКЭаЁСњЖўШЫ__________ЯШЕНДяввЕиЃЌЯШЕН__________ЗжжгЃЎ
ЁОД№АИЁП(1)200Уз/ЗжжгЃЛ(2)(14,2400)ЃЛ(3) s=200t(0ЃМtЁм12)ЃЛ(4)аЁКьЃЌ2Зжжг
ЁОНтЮіЁП
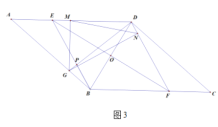
(1)гЩгкаЁСњжаМфанЯЂСЫ2ЗжжгЃЌЖдгІЕФЪЧЭМжаABЖЮЃЌЙЪелЯпOABDЖдгІЕФЪЧаЁСњЕФКЏЪ§ЙиЯЕЭМЯёЃЌEFЪЧаЁКьЖдгІЕФКЏЪ§ЭМЯёЃЌгЩOAЖЮМДПЩЧѓГіаЁСњЦяГЕЫйЖШЃЛ
(2)гЩAЕуКсзјБъМг2МДЕУBЕуКсзјБъЃЌНјЖјЧѓГіBЕузјБъЃЛ
(3)МДЧѓЭМжаOAЖЮе§БШР§КЏЪ§ЫљЖдгІЕФНтЮіЪНМДПЩЃЛ
(4)ЫгУЕФЪБМфЖЬОЭБэЪОЫЯШДяЕНввЕиЃЌгЩЭММДПЩЧѓНт.
НтЃК(1)гЩЭМПЩжЊЃКелЯпOAEDБэЪОаЁСњЕФдЫЖЏЭМаЮЃЌEFБэЪОаЁКьЕФдЫЖЏЭМаЮЃЌ
ЙЪаЁСњЦяГЕЕФЫйЖШЮЊЃК2400ЁТ12=200Уз/ЗжжгЃЛ
ЙЪД№АИЮЊЃК200Уз/ЗжжгЃЛ
(2)гЩЭМПЩжЊЃКAЕузјБъЮЊ(12,2400),
ЁпаЁСњЕНДяМзЕиКѓанЯЂСЫ2ЗжжгЃЌ
ЁрBЕузјБъЮЊ(14,2400)ЃЛ
ЙЪД№АИЮЊЃК(14,2400);
(3)аЁСњДгввЕиЕНМзЕиЃЌЖдгІЕФЪЧЭМжаЯпЖЮOAЃЌ
ЙЪЩшOAЫљдкжБЯпЕФНтЮіЪНЮЊЃКs=kt
ДњШыA(12,2400),МДЃК2400=12k
НтЕУk=200ЃЌ
ЙЪsгыtжЎМфЕФКЏЪ§БэДяЪНЮЊЃКs=200t(0ЃМtЁм12)
ЙЪД№АИЮЊЃКs=200t(0ЃМtЁм12).
(4)аЁКьдкЭМжаFЕуЕНДяввЕиЃЌаЁСњдкЭМжаDЕуЕНДяввЕиЃЌ
ЙЪаЁКьгУЕФЪБМфИќЖЬЃЌ
ЁраЁКьЯШЕНДяввЕи
аЁКьЕФЫйЖШЮЊУПЗжжг100УзЃЌТЗГЬЮЊ2400Уз
ЁраЁКьЕНДяввЕиЫљгУЕФЪБМфЮЊЃК2400ЁТ100=24ЗжжгЃЛ
аЁСњШЅЪБКЭЛиЪБЕФЫйЖШЯрЭЌЃЌОљЮЊ200Уз/ЗжжгЃЌЧвТЗГЬЯрЭЌЃЌ
ЁрЛиРДЫљгаЕФЪБМфКЭШЅЪБЫљгУЪБМфЯрЭЌЃЌЮЊ12ЗжжгЃЌ
МгЩЯжаЭОанЯЂЕФ2ЗжжгЃЌЙЪаЁСњвЛЙВгУЪБЃК12+2+12=26ЗжжгЃЛ
26-24=2ЃЌ
ЁраЁКьБШаЁСњЯШЕН2Зжжг.
ЙЪД№АИЮЊЃКаЁКьЯШЕНввЕиЃЌЯШЕН2Зжжг.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФЗНГЬx2ЉЃЈ2m+1ЃЉx+mЃЈm+1ЃЉ=0ЃЌ
ЃЈ1ЃЉЧѓжЄЃКЗНГЬзмгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЛ
ЃЈ2ЃЉЩшЗНГЬЕФСНИљЗжБ№ЮЊx1ЁЂx2ЃЌЧѓ![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌЦНааЫФБпаЮ![]() жаЃЌЖдНЧЯп
жаЃЌЖдНЧЯп![]() ЕФДЙжБЦНЗжЯпЗжБ№НЛ
ЕФДЙжБЦНЗжЯпЗжБ№НЛ![]() ЁЂ
ЁЂ![]() гкЕу
гкЕу![]() ЁЂ
ЁЂ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЛ
ЃЛ


ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКЫФБпаЮ![]() ЪЧСтаЮЃЛ
ЪЧСтаЮЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ЩЯЃЌСЌНг
ЩЯЃЌСЌНг![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌзї
ЃЌзї![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓЯпЖЮ
ЃЌЧѓЯпЖЮ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтБОаЃЦпФъМЖЭЌбЇдкЫЋанШеВЮМгЬхг§ЖЭСЖЕФЪБМфЃЌПЮЬтаЁзщНјааСЫЮЪОэЕїВщЃЈЮЪОэЕїВщБэШчЭМЫљЪОЃЉЃЌВЂгУЕїВщНсЙћЛцжЦСЫЭМ1ЃЌЭМ2СНЗљЭГМЦЭМЃЈОљВЛЭъећЃЉЃЌЧыИљОнЭГМЦЭМНтД№вдЯТЮЪЬтЃК
 ЃЈ1ЃЉБОДЮНгЪмЮЪОэЕїВщЕФЭЌбЇгаЖрЩйШЫЃПВЙШЋЬѕаЮЭГМЦЭМЃЎ
ЃЈ1ЃЉБОДЮНгЪмЮЪОэЕїВщЕФЭЌбЇгаЖрЩйШЫЃПВЙШЋЬѕаЮЭГМЦЭМЃЎ
ЃЈ2ЃЉБОаЃгаЦпФъМЖЭЌбЇ800ШЫЃЌЙРМЦЫЋанШеВЮМгЬхг§ЖЭСЖЪБМфдк3аЁЪБвдФкЃЈВЛКЌ3аЁЪБЃЉЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЮЇЙХДњЪ§бЇЕФаэЖрДДаТКЭЗЂеЙЖМЮЛОгЪРНчЧАСаЃЌШчФЯЫЮЪ§бЇМвбюЛд(дМ13ЪРМЭ)ЫљжјЕФЁЖЯъНтОХеТЫуЪѕЁЗвЛЪщжаЃЌгУШчЭМЕФШ§НЧаЮНтЪЭЖўЯюКЭ(a+b)ЁАЕФеЙПЊЪНЕФИїЯюЯЕЪ§ЃЌДЫШ§НЧаЮГЦЮЊЁАбюЛдШ§НЧЁБ.

ИљОнЁАбюЛдШ§НЧЁБЧыМЦЫу(a+b)20ЕФеЙПЊЪНжаЕкШ§ЯюЕФЯЕЪ§ЮЊ________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBACЃН30ЁуЃЌвдABЮЊжБОЖЕФЁбOОЙ§ЕуC.Й§ЕуCзїЁбOЕФЧаЯпНЛABЕФбгГЄЯпгкЕуP.ЕуDЮЊдВЩЯвЛЕуЃЌЧв![]() ЃЌЯвADЕФбгГЄЯпНЛЧаЯпPCгкЕуEЃЌСЌНгBCЃЎ
ЃЌЯвADЕФбгГЄЯпНЛЧаЯпPCгкЕуEЃЌСЌНгBCЃЎ
ЃЈ1ЃЉХаЖЯOBКЭBPЕФЪ§СПЙиЯЕ,ВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєЁбOЕФАыОЖЮЊ2ЃЌЧѓAEЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌAЃЈ0ЃЌ4ЃЉЃЌBЃЈ8ЃЌ0ЃЉЃЌCЃЈ8ЃЌ4ЃЉЃЎ
ЃЈ1ЃЉЪдЫЕУїЫФБпаЮAOBCЪЧОиаЮЃЎ
ЃЈ2ЃЉдкxжсЩЯШЁвЛЕуDЃЌНЋЁїDCBШЦЕуCЫГЪБеыа§зЊ90ЁуЕУЕН![]() ЃЈЕу
ЃЈЕу![]() гыЕуDЖдгІЃЉЃЎШєODЃН3ЃЌЧѓЕу
гыЕуDЖдгІЃЉЃЎШєODЃН3ЃЌЧѓЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊxЃН![]() ЃЛ
ЃЛ
ЃЈ1ЃЉЧѓx2+y2ЉxyЕФжЕЃЛ
ЃЈ2ЃЉШєxЕФаЁЪ§ВПЗжЮЊaЃЌyЕФаЁЪ§ВПЗжЮЊbЃЌЧѓЃЈa+bЃЉ2+![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЦЌЙћдАгаЙћЪї80ПУЃЌЯжзМБИЖржжвЛаЉЙћЪїЬсИпВњСП,ЕЋЪЧШчЙћЖржжЪї,ФЧУДЪїжЎМфЕФОрРыКЭУППУЪїЫљЪмЙтееОЭЛсМѕЩй,ЕЅПУЪїЕФВњСПЫцжЎНЕЕЭ.ШєИУЙћдАУППУЙћЪїВњЙћyЃЈЧЇПЫЃЉЃЌдіжжЙћЪї![]() ЃЈПУЃЉЃЌЫќУЧжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪО.
ЃЈПУЃЉЃЌЫќУЧжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪО.
ЃЈ1ЃЉЧѓyгы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЕБдіжжЙћЪїЖрЩйПУЪБЃЌЙћдАЕФзмВњСПwЃЈЧЇПЫЃЉзюДѓЃПзюДѓВњСПЪЧЖрЩйЃП

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com