
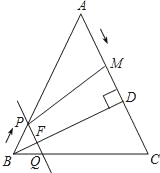
【题目】如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/秒;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/秒,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).
(1)当t为何值时,四边形PQCM是平行四边形?
(2)设四边形PQCM的面积为y(cm2),求y与t之间的函数关系式.
【答案】(1)当t=![]() s时,四边形PQCM是平行四边形;(2)y=
s时,四边形PQCM是平行四边形;(2)y=![]() t2﹣8t+40.
t2﹣8t+40.
【解析】试题分析:(1)假设![]() 为平行四边形,根据平行四边形的性质得到对边平行,进而得到AP=AM,列出关于t的方程,求出方程的解得到满足题意t的值;
为平行四边形,根据平行四边形的性质得到对边平行,进而得到AP=AM,列出关于t的方程,求出方程的解得到满足题意t的值;
(2)根据![]() ,可得△PBQ∽△ABC,根据相似三角形的形状必然相同可知
,可得△PBQ∽△ABC,根据相似三角形的形状必然相同可知![]() 也为等腰三角形,即
也为等腰三角形,即![]() 再由证得的相似三角形得底比底等于高比高,用含
再由证得的相似三角形得底比底等于高比高,用含![]() 的代数式就可以表示出
的代数式就可以表示出![]() ,进而得到梯形的高
,进而得到梯形的高![]() 又点
又点![]() 的运动速度和时间可知点
的运动速度和时间可知点![]() 走过的路程
走过的路程![]() 所以梯形的下底
所以梯形的下底![]() 最后根据梯形的面积公式即可得到
最后根据梯形的面积公式即可得到![]() 与
与![]() 的关系式;
的关系式;
试题解析:(1)假设四边形PQCM是平行四边形,则PM∥QC,
∴AP:AB=AM:AC,
∵AB=AC,
∴AP=AM,即10t=2t,
解得: ![]()
∴当![]() 时,四边形PQCM是平行四边形;
时,四边形PQCM是平行四边形;
(2)∵![]() ,
,
∴△PBQ∽△ABC,
∴△PBQ为等腰三角形,PQ=PB=t,
∴![]() ,即
,即![]()
解得: ![]()
![]()
又∵![]()
![]()


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】郑老师想为希望小学四年(3)班的同学购买学习用品,了解到某商店每个书包的价格比每本词典多8元,用124元恰好可以买到3个书包和2本词典.
(1)每个书包和每本词典的价格各是多少元?
(2)郑老师有1000元,他计划为全班40位同学每人购买一件学习用品(一个书包或一本词典)后,余下不少于100元且不超过120元的钱购买体育用品,共有哪几种购买书包和词典的方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC与△DEF中,给出下列六个条件:(1)AB=DE;(2)BC=EF;(3)AC=DF;(4)∠A=∠D;(5)∠B=∠E;(6)∠C=∠F,以其中三个条件为已知,不能判断△ABC与△DEF全等的是( )
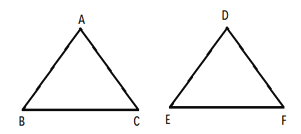
A. (1)(2)(3)B. (1)(2)(5)
C. (1)(4)(6)D. (2)(3)(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,2),且![]() +(a+2b-4)2=0.
+(a+2b-4)2=0.
(1)求a,b的值.
(2)在y轴的正半轴上存在一点M,使S△COM=![]() S△ABC,求出点M的坐标.
S△ABC,求出点M的坐标.
(3)在坐标轴的其他位置是否有在点M,使S△COM=![]() S△ABC仍成立?若存在,请直 接写出符合条件的点M的坐标.
S△ABC仍成立?若存在,请直 接写出符合条件的点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合.将三角尺绕点A按逆时针方向旋转.
(1)当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时,(如图1),通过观察或测量BE,CF的长度,你能得出什么结论并证明你的结论;
(2)当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图2),你在(1)中得到的结论还成立吗?简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各为多少万元?
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,且A型号车不少于2辆,购车费不少于130万元,则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为切实做好校园疫情防控和开学的各项准备工作,某校准备再次购进免手洗消毒凝胶和医用口罩用于防疫,若购进30箱医用口罩和20箱免手洗消毒凝胶共需8500元;若购进40箱医用口罩和10箱免手洗消毒凝胶共需8000元.
(1)求医用口罩和免手洗消毒凝胶每箱购进价格分别为多少元?
(2)若该校购进免手洗消毒凝胶的数量比购进医用口罩数量的2倍少10箱,且用于购置两种物资的总经费不超过9000元,则该校至多购进医用口罩多少箱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连接EF.
(1)求证:∠1=∠F;
(2)若sinB=![]() ,EF=2
,EF=2![]() ,求CD的长.
,求CD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com