
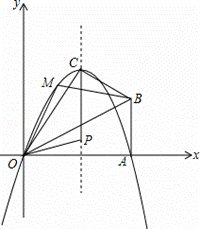
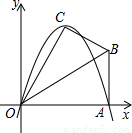
��֪����Rt��OAB�У���OAB=90�㣬��BOA=30�㣬AB=2����O Ϊԭ�㣬OA����ֱ��Ϊx�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵ����B�ڵ�һ�����ڣ���Rt��OAB��OB�۵���A���ڵ�һ�����ڵĵ�C����
��1�����C�������O��C��A����������ߵĽ���ʽ��
��2��P�Ǵ������ߵĶԳ�����һ���㣬����P��O��CΪ������������ǵ���������ʱ����ֱ��д����P�����ꣻ
��3��M��x��y���Ǵ���������һ�����㣬����MOB��������ڡ�OAB���ʱ����M�����꣮
�⣺��1������֪��������֪OC=OA=![]() =2
=2![]() ����COA=60�㣬
����COA=60�㣬
 C���������
C���������![]() ��3����
��3����
���O��A��C����������ߵĽ���ʽΪy=ax2+bx+c��
�� �����
�����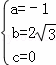 ��
��
���������ߵĽ���ʽΪy=��x2+2![]() x��
x��
��2�������⣬��P��![]() ��y������
��y������
OP2=y2+3��CP2=��y��3��2=y2��6y+9��OC2=12��
�ٵ�OP=CPʱ��6y=6���� y=1��
�ڵ�OP=OCʱ��y2=9���� y=��3��y=3��ȥ����
�۵�CP=OCʱ��y2��6y��3=0���� y=3��2![]() ��
��
��P��������ǣ�![]() ��1����
��1����![]() ����3����
����3����![]() ��3��2
��3��2![]() ����
����![]() ��3+2
��3+2![]() ����
����
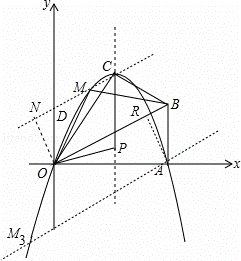
��3����A��AR��OB��R����O��ON��MN��N��MN��y�ύ�ڵ�D��
�ߡ�OAB=90�㣬��BOA=30�㣬AB=2��
��OA=2![]() ��OB=4��
��OB=4��
�������������ʽ�ã�4��AR=2![]() ��2��
��2��
AR=![]() ��
��
�ߡ�MOB��������ڡ�OAB�����
����ֱ��OB���ߣ���OB�ľ������![]() ��ֱ����������ֱ�ߺ������ߵĽ������M�㣬
��ֱ����������ֱ�ߺ������ߵĽ������M�㣬
��NOD=��BOA=30�㣬ON=![]() ��
��
��OD=2��
���ֱ��OB�Ľ���ʽ��y=![]() x��
x��
��������ֱ�ߵĽ���ʽ��y=![]() x+2��y=
x+2��y=![]() x��2��
x��2��
��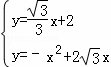 ��
�� ��
��
��ã�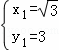 ��
��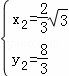 ��
��![]() ��
��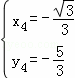
��ʱ��M1��![]() ��3����M2��
��3����M2��![]() ������M3��2
������M3��2![]() ��0����M4����
��0����M4����![]() ��������
��������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
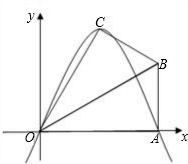 ��Ϊx�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵ����B�ڵ�һ�����ڣ���Rt��OAB��OB�۵���A���ڵ�һ�����ڵĵ�C����
��Ϊx�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵ����B�ڵ�һ�����ڣ���Rt��OAB��OB�۵���A���ڵ�һ�����ڵĵ�C�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
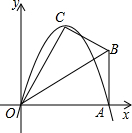 ���ʣ��Ƿ���������ĵ�P��ʹ���ı���CDPMΪ�������Σ������ڣ��������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
���ʣ��Ƿ���������ĵ�P��ʹ���ı���CDPMΪ�������Σ������ڣ��������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
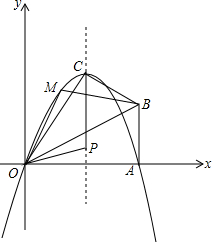 ��2013•�人ģ�⣩��֪����Rt��OAB�У���OAB=90�㣬��BOA=30�㣬AB=2����O Ϊԭ�㣬OA����ֱ��Ϊx�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵ����B�ڵ�һ�����ڣ���Rt��OAB��OB�۵���A���ڵ�һ�����ڵĵ�C����
��2013•�人ģ�⣩��֪����Rt��OAB�У���OAB=90�㣬��BOA=30�㣬AB=2����O Ϊԭ�㣬OA����ֱ��Ϊx�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵ����B�ڵ�һ�����ڣ���Rt��OAB��OB�۵���A���ڵ�һ�����ڵĵ�C�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2013•����ˮ����֪����Rt��OAB�У���OAB=90�㣬��BOA=30�㣬OA=2
��2013•����ˮ����֪����Rt��OAB�У���OAB=90�㣬��BOA=30�㣬OA=2| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����34�¡����κ����������⼯��23����34.4 ���κ�����Ӧ�ã������棩 ���ͣ������
 ���Գ��ṫʽΪx=-
���Գ��ṫʽΪx=-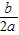 ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com