
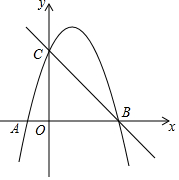
 如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax+3与x轴交于A、B两点,与y轴交于点C,过B、C两点的直线解析式为y=-x+b.
如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax+3与x轴交于A、B两点,与y轴交于点C,过B、C两点的直线解析式为y=-x+b.分析 (1)利用抛物线的解析式求出点C坐标,即可求出b,推出点A、B两点坐标,利用待定系数法即可求出a.
(2)如图1中,作PE⊥AB于F,交BC于E.设P(t,-t2+2t+3),则E(t,-t+3).首先证明△PDE是等腰直角三角形,推出PD=$\frac{\sqrt{2}}{2}$PE,由此即可解决问题.
(3)如图2中,设BN的垂直平分线交x轴于H,抛物线的对称轴交x轴于D,作ML⊥GH于L.首先证明cos∠GML=cos∠GAH=$\frac{4}{5}$,由$\frac{3}{4}$AH=GH,列出方程即可解决问题.
解答 解:(1)∵抛物线y=ax2-2ax+3与y轴交于点C,
∴C(0,3)
∵直线解析式为y=-x+b过B、C.
∴C(0,b),B(b,0),
∴b=3,
∴B(3,0),
∵抛物线的对称轴为x=1,A、B关于对称轴对称,
∴A(-1,0),把A(-1,0)代入抛物线的解析式3a+3=0,
∴a=-1,
∴抛物线的解析式为:y=-x2+2x+3;
(2)如图1中,作PE⊥AB于F,交BC于E.设P(t,-t2+2t+3),则E(t,-t+3).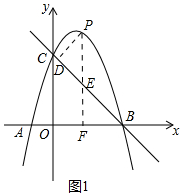
∵OC=OB=3,∠COB=90°,
∴∠COB=∠EFB=90°,
∴∠FEB=∠PED=45°,
∴d=PD=$\frac{\sqrt{2}}{2}$PE=$\frac{\sqrt{2}}{2}$(-t2+2t+3+t-3)=-$\frac{\sqrt{2}}{2}$t2+$\frac{3\sqrt{2}}{2}$t.(0<t<3).
∴d=-$\frac{\sqrt{2}}{2}$t2+$\frac{3\sqrt{2}}{2}$t.(0<t<3).
(3)如图2中,设BN的垂直平分线交x轴于H,抛物线的对称轴交x轴于D,作ML⊥GH于L.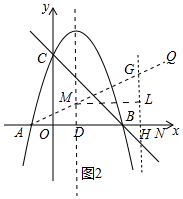
∵GM:AN=5:8,设GM=5k,AN=8k,
∵AB=4,BD=2,
∴BN=8k-4,
BH=4k-2,
DH=DB+BH=4k,
∴cos∠GML=$\frac{ML}{MG}$=$\frac{4}{5}$,
∵ML∥AH,
∴∠GML=∠GAH,
∴cos∠GAH=$\frac{4}{5}$,
∴$\frac{3}{4}$AH=GH,
设G点横坐标为m,
∵点G关于x轴的对称点恰好在抛物线上,
∴G(m,m2-2m-3),
∴$\frac{3}{4}$(m+1)=m2-2m-3,
解得m=$\frac{15}{4}$或-1(舍弃),
∴点H($\frac{15}{4}$,0),N($\frac{9}{2}$,0).
∵d=-$\frac{\sqrt{2}}{2}$t2+$\frac{3\sqrt{2}}{2}$t=-$\frac{\sqrt{2}}{2}$(t-$\frac{3}{2}$)2+$\frac{9\sqrt{2}}{8}$,
∵-$\frac{\sqrt{2}}{2}$<0,
∴t=$\frac{3}{2}$时,d有最大值,此时P($\frac{3}{2}$,$\frac{15}{4}$),
∴此时直线PN与x轴所夹锐角的正切值=$\frac{\frac{15}{4}}{\frac{9}{2}-\frac{3}{2}}$=$\frac{5}{4}$.
点评 本题考查二次函数综合题、等腰直角三角形的性质、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会构建二次函数解决最值问题,学会利用参数解决问题,属于中考压轴题.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
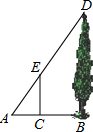 如图,某学生想利用标杆测量一棵大树的高度,如果标杆EC的高为1.8m,并测得AC=0.9m,AB=2.1m,那么大树DB的高度是4.2m.
如图,某学生想利用标杆测量一棵大树的高度,如果标杆EC的高为1.8m,并测得AC=0.9m,AB=2.1m,那么大树DB的高度是4.2m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com