
【题目】已知:如图,![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() 平分
平分![]() ,且
,且![]() 于
于![]() ,与
,与![]() 相交于点
相交于点![]()
(1)求证:![]() ; (2)求证:
; (2)求证:![]() ;
;
(3)取![]() 边的中点
边的中点![]() ,连结
,连结![]() 、
、![]() 、
、![]() ,取
,取![]() 的中点G,连结
的中点G,连结![]() ,说明GH与DE的位置关系.
,说明GH与DE的位置关系.

【答案】(1)见解析;(2)见解析;(3)GH⊥DE,理由见解析.
【解析】
(1)根据等腰直角三角形的性质可得DB=DC,根据同角的余角相等可得∠DBF=∠ACD,然后利用ASA证明△ADC≌△FDB即可得到BF=AC;
(2)根据等角的余角相等可得∠A=∠BCA,进而得到BA=BC,根据等腰三角形的性质(三线合一),可得AE=EC=![]() AC=
AC=![]() BF;
BF;
(3)根据直角三角形斜边上的中线等于斜边的一半可证明DH=EH,然后根据等腰三角形的性质(三线合一)可得结论.
(1)∵∠ABC=45°,CD⊥AB于D,
∴∠DBC=∠DCB=45°,
∴DB=DC,
∵BE⊥AC,
∴∠AEB=∠ADC=90°,
∴∠A+∠ABE=90°,∠A+ACD=90°,
∴∠DBF=∠ACD,
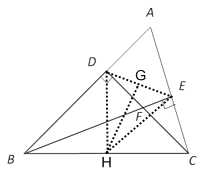
在△ADC和△FDB中,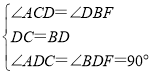 ,
,
∴△ADC≌△FDB(ASA),
∴BF=AC;
(2)∵∠ABE=∠CBE,∠ABE+∠A=90°,∠CBE+∠BCA=90°,
∴∠A=∠BCA,
∴BA=BC,
∵BE⊥AC,
∴AE=CE,
∵AC=BF,
∴CE=![]() BF;
BF;
(3)GH⊥DE,
理由:如图,
∵在Rt△BDC和Rt△BEC中,H为BC中点,
∴DH=![]() BC,EH=
BC,EH=![]() BC,
BC,
∴DH=EH,
∵G为DE中点,
∴GH⊥DE.


科目:初中数学 来源: 题型:
【题目】取一副三角板按如图所示拼接,固定三角板ADC,将三角板ABC绕点A顺时针方向旋转,旋转角度为α(0°<α≤45°),得到△ABC′.

①当α为多少度时,AB∥DC?
②当旋转到图③所示位置时,α为多少度?
③连接BD,当0°<α≤45°时,探求∠DBC′+∠CAC′+∠BDC值的大小变化情况,并给出你的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
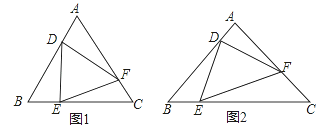
【题目】定义:在△ABC中,点D,E,F分别是边AB,BC,CA上的动点,若△DEF∽△ABC(点D、E、F的对应点分别为点A、B、C),则称△DEF是△ABC的子三角形,如图.
(1)已知:如图1,△ABC是等边三角形,点D,E,F分别是边AB,BC,CA上动点,且AD=BE=CF.
求证:△DEF是△ABC的子三角形.
(2)已知:如图2,△DEF是△ABC的子三角形,且AB=AC,∠A=90°,若BE=![]() ,求CF和AD的长.
,求CF和AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形.如图②,将四边形ACBD折叠,使D与C重合,EF为折痕,若BC=2,则AE的值为()

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答问题
(2x﹣5)2+(3x+7)2=(5x+2)2
解:设m=2x﹣5,n=3x+7,则m+n=5x+2
则原方程可化为m2+n2=(m+n)2
所以mn=0,即(2x﹣5)(3x+7)=0
解之得,x1=![]() ,x2=﹣
,x2=﹣![]()
请利用上述方法解方程(4x﹣5)2+(3x﹣2)2=(x﹣3)2
查看答案和解析>>
科目:初中数学 来源: 题型:
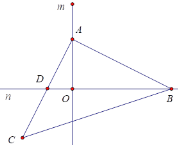
【题目】如图,直线m⊥n,等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、点B分别是m、n上两个动点,直角边AC交直线n于点D,斜边BC交直线m于点E.
(1)如图(1)求证:∠DAO=∠ABO;
(2)如图(2),当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE;
(3)如图(3),分别以OB、AB为直角边作等腰直角△BOD和等腰直角△ABC,连结CD交直线n于点P,求![]() 的值.
的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,东营市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=4,∠BAC=120°,M是BC的中点,点E是AB边上的动点,点F是线段BM上的动点,则ME+EF的最小值等于___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E、F分别在AC和BC上,则CE:CF的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com