Question

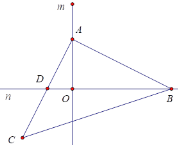
【题目】如图，直线m⊥n，等腰Rt△ABC中，∠BAC＝90°，AB＝AC，点A、点B分别是m、n上两个动点，直角边AC交直线n于点D，斜边BC交直线m于点E．

（1）如图（1）求证：∠DAO＝∠ABO；

（2）如图（2），当等腰Rt△ABC运动到使点D恰为AC中点时，连接DE，求证：∠ADB＝∠CDE；

（3）如图（3），分别以OB、AB为直角边作等腰直角△BOD和等腰直角△ABC，连结CD交直线n于点P，求的值．

Answer 1

【答案】（1）见解析；（2）见解析；（3）.

【解析】

（1）根据题意可得∠ABO+∠BAO＝90°，∠DAO+∠BAO＝90°，利用同角的余角相等可得结论；

（2）作CG⊥AC交m与点G，首先利用ASA证明△ADB≌△CGA，可得AD=CG，进而得到CG=CD，然后证明△DCE≌△GCE，可得∠CDE=∠CGE，等量代换即可得到结论；

（3）作CF⊥n于点F，根据“一线三等角”模型易证△ABO≌△BCF，可得OB=FC，AO=BF，然后结合△BOD是等腰直角三角形证明△DBP≌△CFP，得到BP=FP，最后利用三角形面积公式计算化简即可.

解：（1）∵直线m⊥n，

∴∠AOD＝∠AOB＝90°，

∴∠ABO+∠BAO＝90°，

∵∠BAC＝90°，

∴∠DAO+∠BAO＝90°，

∴∠DAO＝∠ABO；

（2）作CG⊥AC交m与点G，则∠ACG＝90°，

在△ADB和△CGA中，，

∴△ADB≌△CGA（ASA），

∴AD=CG，

∵AD=CD，

∴CG=CD，

∵∠ACB=45°，

∴∠GCE=45°，

∴∠ACB=∠GCE，

又∵CE=CE，

∴△DCE≌△GCE（SAS），

∴∠CDE=∠CGE，

∵△ADB≌△CGA，

∵∠CGE=∠ADB，

∴∠ADB＝∠CDE；

（3）作CF⊥n于点F，则∠CFB=90°，

∴∠CBF+∠BCF=90°，

∵△ABC是等腰直角三角形，

∴∠ABC=90°，AB=BC，

∴∠ABO+∠CBF=90°，

∴∠BCF=∠ABO，

在△ABO和△BCF中，，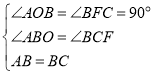

∴△ABO≌△BCF（AAS），

∴OB=FC，AO=BF，

∵△BOD是等腰直角三角形，

∴OB=BD，∠OBD=∠DBP=90°，

∴BD=FC，

在△DBP和△CFP中，，

∴△DBP≌△CFP（AAS），

∴BP=FP，

∴.