【题目】在平面内由极点、极轴和极径组成的坐标系叫做极坐标系．如图，在平面上取定一点O称为极点；从点O出发引一条射线Ox称为极轴；线段OP的长度称为极径．点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度（规定逆时针方向转动角度为正）来确定，即P（3，60°）或P（3，﹣300°）或P（3，420°）等，则点P关于点O成中心对称的点Q的极坐标表示不正确的是（ ）
A. Q（3，240°） B. Q（3，﹣120°） C. Q（3，600°） D. Q（3，﹣500°）
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，CE是ABCD的边AB的垂直平分线，垂足为点O，CE与DA的延长线交于点E．连接AC，BE，DO，DO与AC交于点F，则下列结论：
①四边形ACBE是菱形；
②∠ACD=∠BAE；
③AF：BE=2：3；
④S四边形AFOE：S△COD=2：3．
其中正确的结论有_____．（填写所有正确结论的序号）
查看答案和解析>>
科目：初中数学 来源： 题型：
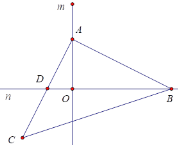
【题目】如图，直线m⊥n，等腰Rt△ABC中，∠BAC＝90°，AB＝AC，点A、点B分别是m、n上两个动点，直角边AC交直线n于点D，斜边BC交直线m于点E．
（1）如图（1）求证：∠DAO＝∠ABO；
（2）如图（2），当等腰Rt△ABC运动到使点D恰为AC中点时，连接DE，求证：∠ADB＝∠CDE；
（3）如图（3），分别以OB、AB为直角边作等腰直角△BOD和等腰直角△ABC，连结CD交直线n于点P，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面的例题及点拨，补全解题过程（完成点拨部分的填空），并解决问题：例题：如图1，在等边△ABC中，M是BC边上一点（不含端点B，C），N是△ABC的外角∠ACH的平分线上一点，且AM＝MN．求证：∠AMN＝60°
点拨：如图2，作∠CBE＝60°，BE与NC的延长线相交于点E，得等边△BEC，连结EM，易证△ABM≌△EBM（ ），可得AM＝EM，∠1＝∠2；又AM＝MN，则EM＝MN，可得∠ ＝∠ ；
由∠3+∠1＝∠4+∠5＝60°，进一步可得∠1＝∠2＝∠ ．
又因为∠2+∠6＝120，所以∠5+∠6＝120°，所以∠AMN＝60°．
问题：如图3，四边形ABCD的四条边都相等，四个角都等于90°，M是BC边上一点（不含端点B，C），N是四边形ABCD的外角∠DCH的平分线上一点，且AM＝MN．求∠AMN的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC=4，∠BAC=120°，M是BC的中点，点E是AB边上的动点，点F是线段BM上的动点，则ME+EF的最小值等于___.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】点O是平行四边形ABCD的对称中心，AD＞AB，E、F分别是AB边上的点，且EF＝
AB；G、H分别是BC边上的点，且GH＝
BC；若S1,S2分别表示EOF和GOH的面积，则S1,S2之间的等量关系是______________
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将Rt△ABC沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，且∠EAF=
∠DAB．试猜想DE，BF，EF之间有何数量关系，并证明你的猜想．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，水库大坝的横截面是梯形，坝顶宽5米，CD的长为20
米，斜坡AB的坡度i＝1：2.5（i为坡比即BE：AE），斜坡CD的坡度i＝1：2（i为坡比即CF：FD），求坝底宽AD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将三角形纸片ABC沿AD折叠，使点C落在BD边上的点E处．若BC＝8，BE＝2．则AB2﹣AC2的值为（ ）
A. 4 B. 6 C. 10 D. 16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
