
分析 (1)(2)分子是1,分母是相差3的两个自然数的乘积,等于分子是1,分母是这两个自然数的两个分数差的$\frac{1}{3}$,由此规律解决问题;
(3)利用得出的规律拆分计算即可;
(4)把问题转化为ap+ap+1+ap+2+…+ap+q=(a1+a2+a3+a4+…+ap+ap+1+ap+2+…+ap+q)-(a1+a2+a3+a4+…+ap-1)得出答案即可.
解答 解:(1)a5=$\frac{1}{13×16}$=$\frac{1}{3}$×($\frac{1}{13}$-$\frac{1}{16}$);
(2)用含n(n为正整数)的式子表示第n个等式:an=$\frac{1}{(3n-2)(3n+1)}$=$\frac{1}{3}$($\frac{1}{3n-2}$-$\frac{1}{3n+1}$).
(3)a1+a2+a3+a4+…+a100
=$\frac{1}{1×4}$+$\frac{1}{4×7}$+$\frac{1}{7×10}$+…+$\frac{1}{298×301}$
=$\frac{1}{3}$×(1-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{7}$+$\frac{1}{7}$-$\frac{1}{10}$+…+$\frac{1}{298}$-$\frac{1}{301}$)
=$\frac{1}{3}$×(1-$\frac{1}{301}$)
=$\frac{100}{301}$;
(4)ap+ap+1+ap+2+…+ap+q
=(a1+a2+a3+a4+…+ap+ap+1+ap+2+…+ap+q)-(a1+a2+a3+a4+…+ap-1)
=$\frac{1}{3}$(1-$\frac{1}{3(p+q)+1}$)-$\frac{1}{3}$(1-$\frac{1}{3(p-1)+1}$)
=$\frac{1}{3}$($\frac{1}{3(p-1)+1}$-$\frac{1}{3(p+q)+1}$).
点评 此题考查数字的变化规律,找出数字之间的联系,得出运算规律,利用规律解决问题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
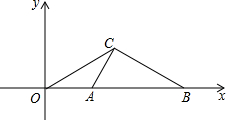 如图,已知点A(2,0),B(6,0),∠ACB是直角,△OCA∽△OBC.
如图,已知点A(2,0),B(6,0),∠ACB是直角,△OCA∽△OBC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{14}{3}$ | D. | $\frac{20}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com