练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在一个不透明的袋子里装有3个黑球和若干白球，它们除颜色外都相同．在不允许将球倒出来数的前提下，小明为估计其中白球数，采用如下办法：随机从中摸出一球，记下颜色后放回袋中，充分摇匀后，再随机摸出一球，记下颜色，…不断重复上述过程．小明共摸100次，其中20次摸到黑球．根据上述数据，小明估计口袋中白球大约有()
    A.10个
    B.12 个
    C.15 个
    D.18个

    【答案】B
    【解析】解答：∵小明共摸了100次，其中20次摸到黑球，
    ∴有80次摸到白球，∴摸到黑球与摸到白球的次数之比为1：4，
    ∴口袋中黑球和白球个数之比为1：4，3÷ =12（个）．
    故选B．
    分析:在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近，可以从比例关系入手，列出算式解答．
    【考点精析】解答此题的关键在于理解用频率估计概率的相关知识，掌握在同样条件下，做大量的重复试验，利用一个随机事件发生的频率逐渐稳定到某个常数，可以估计这个事件发生的概率．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

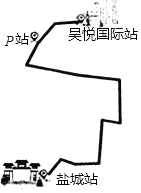
    【题目】常州每年举行一次“一袋牛奶的暴走”公益活动，用步行的方式募集善款，其中挑战型路线”的起点是淹城站，并沿着规定的线路到达终点吾悦国际站．甲、乙两组市民从起点同时出发，已知甲组的速度为6km/h，乙组的速度为5km/h，当甲组到达终点后，立即以3km/h的速度按原线路返回，并在途中的P站与乙组相遇，P站与吾悦国际站之间的路程为1.5km

    （1）求“挑战型路线”的总长；

    （2）当甲组到达终点时，乙组离终点还有多少路程？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小兰和小潭分别用掷A、B两枚骰子的方法来确定P(x，y)的位置，她们规定：小兰掷得的点数为x，小谭掷得的点数为y，那么，她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为()
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“十一”黄金周期间，小明要与父母外出游玩，带了2件上衣和3条长裤(把衣服和裤子分别装在两个袋子里)，上衣颜色有红色、黄色，长裤有红色、黑色、黄色．
    问题为：
    （1）小明随意拿出一条裤子和一件上衣配成一套，用(画树状图或列表格)中的一种列出所有可能出现结果；
    （2）配好一套衣服，小明正好拿到黑色长裤的概率是多少；
    （3）他任意拿出一件上衣和一条长裤穿上的颜色正好相同的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

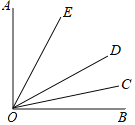
    【题目】如图，已知∠AOB内部有三条射线，OE平分∠AOD，OC平分∠BOD．

    （1）若∠AOB=90°，求∠EOC的度数；

    （2）若∠AOB=α，求∠EOC的度数；

    （3）如果将题中“平分”的条件改为∠EOA=∠AOD，∠DOC=∠DOB，∠AOD=50°，且∠AOB=90°，求∠EOC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某玩具店进了一排黑白塑料球，共5箱，每箱的规格、数量都相同，其中每箱中装有黑白两种颜色的塑料球共3000个，为了估计每箱中两种颜色球的个数，随机抽查了一箱，将箱子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回箱子中，多次重复上述过程后，发现摸到黑球的概率在0.8附近波动，则此可以估计这批塑料球中黑球的总个数，请将黑球总个数用科学记数法表示约为个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料： 在学习《圆》这一章时，老师给同学们布置了一道尺规作图题：


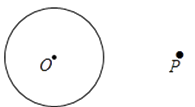
    小敏的作法如下：
    如图，
    ①链接op，做线段op的垂直平分线MN,交OP于点C
    ②以点C为圆心，CO的长为半径作圆，交⊙O于A、B两点
    ③作直线PA、PB所以直线PA,PB就是所求的切线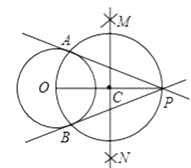

    老师认为小敏的作法正确．
    请回答：连接OA，OB后，可证∠OAP=∠OBP=90°，其依据是；由此可证明直线PA，PB都是⊙O的切线，其依据是

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，⊙O的半径为1，P是坐标系内任意一点，点P到⊙O的距离SP的定义如下：若点P与圆心O重合，则SP为⊙O的半径长；若点P与圆心O不重合，作射线OP交⊙O于点A，则SP为线段AP的长度． 图1为点P在⊙O外的情形示意图．

    （1）若点B（1，0），C（1，1）， ，则SB=；SC=；SD=；
    （2）若直线y=x+b上存在点M，使得SM=2，求b的取值范围；
    （3）已知点P，Q在x轴上，R为线段PQ上任意一点．若线段PQ上存在一点T，满足T在⊙O内且ST≥SR ， 直接写出满足条件的线段PQ长度的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bx+c（a≠0）的图象如图，下列4个结论中结论正确的有 ．
    ①abc＜0；②b＜a+c；③4a+2b+c＞0；④b2﹣4ac＞0．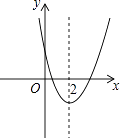

    查看答案和解析>>

    同步练习册答案