
【题目】在平面直角坐标系xOy中,⊙O的半径为1,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若点P与圆心O重合,则SP为⊙O的半径长;若点P与圆心O不重合,作射线OP交⊙O于点A,则SP为线段AP的长度. 图1为点P在⊙O外的情形示意图.
(1)若点B(1,0),C(1,1), ![]() ,则SB=;SC=;SD=;
,则SB=;SC=;SD=;
(2)若直线y=x+b上存在点M,使得SM=2,求b的取值范围;
(3)已知点P,Q在x轴上,R为线段PQ上任意一点.若线段PQ上存在一点T,满足T在⊙O内且ST≥SR , 直接写出满足条件的线段PQ长度的最大值.
【答案】
(1)0;![]() ﹣1;
﹣1;![]()
(2)解:设直线y=x+b与分别与x轴、y轴交于F、E,
作OG⊥EF于G,
∵∠FEO=45°,
∴OG=GE,
当OG=3时,GE=3,
由勾股定理得,OE=3 ![]() ,
,
此时直线的解析式为:y=x+3 ![]() ,
,
∴直线y=x+b上存在点M,使得SM=2,b的取值范围是﹣3 ![]() ≤b≤3
≤b≤3 ![]()
(3)解:∵T在⊙O内,
∴ST≤1,
∵ST≥SR,
∴SR≤1,
∴线段PQ长度的最大值为1+2+1=4.

【解析】解:(1)∵点B(1,0), ∴SB=0,
∵C(1,1),
∴SC= ![]() ﹣1,
﹣1,
∵ ![]() ,
,
∴SD= ![]() ,
,
故答案为:0; ![]() ﹣1;
﹣1; ![]() ;
;
(1)根据点的坐标和新定义解答即可;(2)根据直线y=x+b的特点,结合SM=2,根据等腰直角三角形的性质解答;(3)根据T在⊙O内,确定ST的范围,根据给出的条件、结合图形求出满足条件的线段PQ长度的最大值.


科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有3个黑球和若干白球,它们除颜色外都相同.在不允许将球倒出来数的前提下,小明为估计其中白球数,采用如下办法:随机从中摸出一球,记下颜色后放回袋中,充分摇匀后,再随机摸出一球,记下颜色,…不断重复上述过程.小明共摸100次,其中20次摸到黑球.根据上述数据,小明估计口袋中白球大约有()
A.10个
B.12 个
C.15 个
D.18个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,足球是世界上第一大运动,你热爱足球运动吗?已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一队共踢了30场比赛,负了9场,共得47分,那么这个队胜了( )
A. 10场 B. 11场 C. 12场 D. 13场
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料: 如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2= ![]() 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.
观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2 , 即通过观察函数的图象,可以得到不等式ax+b> ![]() 的解集.
的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.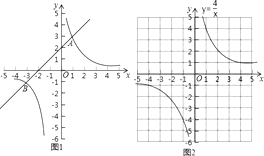
下面是他的探究过程,请将(2)、(3)、(4)补充完整:
(1)①将不等式按条件进行转化: 当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x﹣1> ![]() ;
;
当x<0时,原不等式可以转化为x2+4x﹣1< ![]() ;
;
②构造函数,画出图象
设y3=x2+4x﹣1,y4= ![]() ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
双曲线y4= ![]() 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
(2)确定两个函数图象公共点的横坐标 观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为
(3)借助图象,写出解集 结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
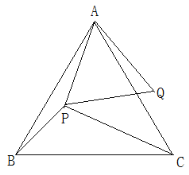
【题目】已知,点P是等边△ABC内一点,PA=4,PB=3,PC=5.线段AP绕点A逆时针旋转60°到AQ,连接PQ.(1)求PQ的长。(2)求∠APB的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
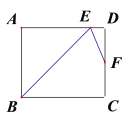
【题目】如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,当点F是CD的中点时,若AB=4,则BC=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙O的半径为1,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若点P与圆心O重合,则SP为⊙O的半径长;若点P与圆心O不重合,作射线OP交⊙O于点A,则SP为线段AP的长度. 图1为点P在⊙O外的情形示意图.
(1)若点B(1,0),C(1,1), ![]() ,则SB=;SC=;SD=;
,则SB=;SC=;SD=;
(2)若直线y=x+b上存在点M,使得SM=2,求b的取值范围;
(3)已知点P,Q在x轴上,R为线段PQ上任意一点.若线段PQ上存在一点T,满足T在⊙O内且ST≥SR , 直接写出满足条件的线段PQ长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为 . 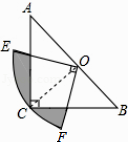
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com