
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

A. 36=15+21 B. 25=9+16 C. 13=3+10 D. 49=18+31
科目:初中数学 来源: 题型:
【题目】阅读填空,并完成问题:“绝对值”一节学习后,数学老师对同学们的学习进行了拓展.数学老师向同学们提出了这样的问题:“在数轴上,一个数的绝对值就是表示这个数的点到原点的距离.那么,如果用P(a)表示数轴上的点P表示有理数a,Q(b)表示数轴上的点Q表示有理数b,那么点P与点Q的距离是多少?”
(1)聪明的小明经过思考回答说:这个问题应该有两种情况.一种是点P和点Q在原点的两侧,此时点P与点Q的距离是a和b的绝对值的和,即∣a∣+∣b∣.例如:点A(-3)与点B(5)的距离为∣-3∣+∣-5∣= ;
另一种是点P和点Q在原点的同侧,此时点P与点Q的距离的a和b中,较大的绝对值减去较小的绝对值,即∣a∣-∣b∣或∣b∣-∣a∣.例如:点A(-3)与点B(-5)的距离为∣-5∣-∣-3∣= ;
你认为小明的说法有道理吗?如果没有道理,请你指出错误之处;如果有道理,请你模仿求出数轴上点M(![]() )与N(
)与N(![]() )之间和点C(-2)与D(-7)之间的距离.
)之间和点C(-2)与D(-7)之间的距离.
(2)小颖在听了小明的方法后,提出了不同的方法,小颖说:我们可以不考虑点P和点Q所在的位置,无论点P与点Q的位置如何,它们之间的距离就是数a与b的差的绝对值,即∣a-b∣.例如:点A(-3)与点B(5)的距离就是∣-3-5∣= ;点A(-3)与点B(-5)的距离就是∣(-3)-(-5)∣= ;你认为小颖的说法有道理吗?如果没有道理,请你指出错误之处;如果有道理,请你模仿求出数轴上点M(![]() )与N(
)与N(![]() )之间和点C(-1.5)与D(-3.5)之间的距离.
)之间和点C(-1.5)与D(-3.5)之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示∠AOB的纸片,OC平分∠AOB,如图2把∠AOB沿OC对折成∠COB(OA与OB重合),从O点引一条射线OE,使∠BOE=![]() ∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.
∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D. 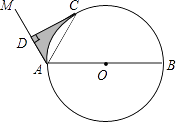
(1)求证:CD是⊙O的切线;
(2)若∠ACD=30°,AD=4,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果保留根号)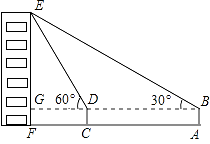
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形纸片ABCD中,AD//BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C处,折痕DE交BC于点E,连结C′E.
求证:四边形CDC′E是菱形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com